Файл: Математическое моделирование в экологии.doc

Термин «параметр» обычно относится к характеристикам, численные значения которых отличаются меньшей определенностью, чем у констант, но, тем не менее, остаются неизменными на протяжении исследования модели. Значения параметров подвержены влиянию условий эксперимента, и они могут иметь приближенное значение.

Для обозначения параметров и констант введем символ Р, а величины, относящиеся к параметрам, будем записывать с индек- сом с, например, S_c — постоянные затраты (с - от const).

Для обозначения переменных введем символы Х, Y, Z и т.д. Величины, относящиеся к переменным, будем записывать с индек- сом v, например, S_v — переменные затраты и т.д. (здесь индекс v — от var).

Подгонка моделей связана с такой корректировкой значений пара- метров Р и начальных условий переменных Х_i (i =1, n), которая прибли- жала бы модель к описываемой ею реальной системе при сохранении выбранной структуры и базовых уравнений. Например, пусть у реальной системы измеряется конкретная характеристика Y_n, в определенные моменты времени t₁, t₂, ..., t_n и соответственно фиксируются значения у₁, у₂, ..., у_n. При тех же условиях по модели фиксируем состояния Y₁,Y₂, ..., Y_n, где Y_i — прогнозируемые величины характеристик системы. Если имеется разница между значениями у_i и У_i, то ее величина называется невязкой и обозначается как

И можно вычислить сумму квадратов невязок

где а_i — некоторый весовой коэффициент, который применяется в случае, когда невязки r_i имеют разную качественную значимость. При этом

а₁ + а₂ +...+ a_n = l.

Сумма невязок используется в качестве меры близости модели к ее прототипу и может быть разбита на две составляющие

R = R_ад +R_е

где R_ад — отражает неадекватность модели прототипу;

R_е — ошибки в экспериментальных данных.

Величина R рассматривается как зависимая от параметров сис- темы Р_1, Р_2, ..., Р_k поэтому ожидаемое значение R_е определяется по формуле

R_е =(n — k) σ²,

где n — число измерений;

k — число параметров;

σ ² — дисперсия ошибки.

Зависимость R от параметров Р_i (i =1, k) может быть записана как

R=R(P₁,P₂,..., P_k)

Для определения минимума функции R(P) используют методы: наименьших квадратов, градиентный и др.

В качестве критерия чувствительности модели, где величина Y_i. прогнозируется в заданный момент времени и известен параметр, от которого зависит эта величина, рекомендуется безразмерная вели- чина

где σ P_i — малое приращение параметра;

σY_i — приращение Y_i вследствие изменения параметра P_i

Параметры, для которых S(Y_i, Р_i) >1, сильно влияют на выход- ной показатель, и наоборот.

2.2. Этапы построения математической модели

При построении математической модели системы можно выделить несколько этапов (рис. 2.1):

I-й этап. Постановка задачи. Этапу предшествует возникновение ситуаций или проблем, осознание которых приводит к мысли их обобщения или решения для последующего достижения, какого- либо эффекта. Исходя из этого, объект описывается, отмечаются вопросы, подлежащие решению, и ставится цель исследования. Здесь необходимо уяснить, что мы хотим получить в результате исследований. Предварительно нужно оценить, нельзя ли получить эти результаты другим, более дешевым или доступным путем.

Рис.(2.1.) Последовательность процесса моделирования

II-й этап. Определение задачи. Исследователь старается определить, к какому виду относится объект, описывает параметры состояния объекта, переменные, характеристики, факторы внешней среды. Необходимо познать закономерности внутренней организации объекта, очертить границы объекта, построить его структуру. Эта работа называется идентификацией системы. Отсюда выбирается задача исследования, которая может решать вопросы: оптимизации, сравнения, оценки, прогноза, анализа чувствительности, выявления функциональных соотношений и т.п.

Следующая работа связана, с разработкой концептуальной мо- дели. Например, для создания системы очистки воды концептуальная модель системы приведена на рис. (2.2.).

Концептуальная модель позволяет оценить положение системы во внешней среде, выявить необходимые ресурсы для ее функционирования, влияние факторов внешней среды и то, что мы ожидаем на выходе.

Необходимость проведения исследования возникает из реальных ситуаций, складывающихся в процессе работы системы, когда они в чем-либо начинают не удовлетворять каким-либо старым или новым требованиям. Если недостатки очевидны и известны методы их уст- ранения, то нет необходимости в исследованиях.

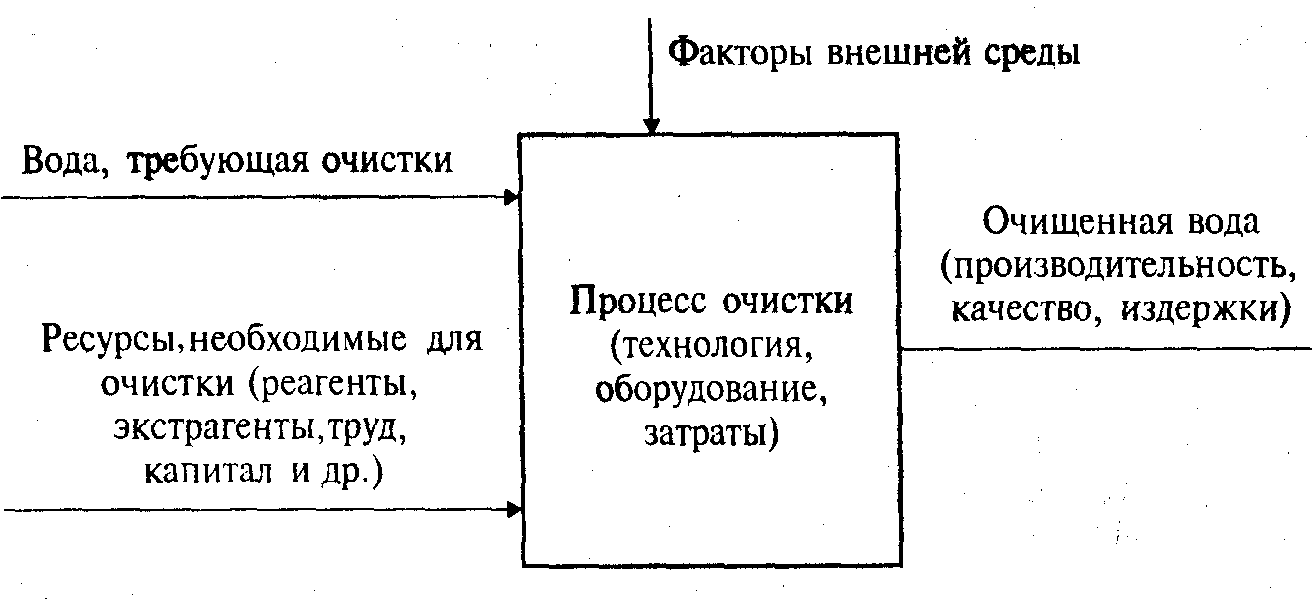
Рис (2.2.) Схема концептуальной модели системы очистки.

К сожалению, такая ситуация встречается достаточно редко. В силу сложности систем и достаточно большого числа факторов, влияющих на эффективность их действия, поставить «диагноз» системе не всегда просто. Изучение сложившейся ситуации, поведения системы и ее элементов, опыт исследователя и его интуиция позволяют поставить предварительный «диагноз» системе, определить и сформулировать задачу исследования.

Исходя из задачи исследования, можно определить назначение математической модели, которая должна быть построена для исследования. Такие модели могут решать задачи:

• выявления функциональных соотношений, заключающихся в определении количественных зависимостей между входными фактора- ми модели и выходными характеристиками исследуемого объекта;

• анализа чувствительности, заключающегося в установлении факторов, которые в большей степени влияют на интересующие ис- следователя выходные характеристики системы;

• прогноза — оценки поведения системы при некотором предполагаемом сочетании внешних условий;

• оценки — определения, насколько хорошо исследуемый объект будет соответствовать некоторым критериям;

• сравнения, заключающегося в сопоставлении ограниченного числа альтернативных вариантов систем или же в сопоставлении нескольких предлагаемых принципов или методов действия;

• оптимизации, состоящей в точном определении такого сочетания переменных управления, при которых обеспечивается экстремальное значение целевой функции.

Выбор задачи определяет процесс создания и экспериментальной проверки модели.

Любое исследование должно начинаться с построения плана, включающего обследование системы и анализ ее функционирования. В плане должны быть предусмотрены:

• описание функций, реализуемых объектом; • определение взаимодействий всех систем и элементов объекта;

• определение зависимости между входными и выходными переменными и влияние переменных управляющих воздействий на эти зависимости;

• определение экономических показателей функционирования системы.

Результаты обследования системы и окружающей среды представляются в виде описания процесса функционирования, которое используется для идентификации системы. Идентифицировать систему — значит выявить и изучить ее, а также:

получить более полную характеристику системы и ее поведения;

познать объективные закономерности ее внутренней организации;

очертить ее границы; указать на вход, процесс и выход; определить ограничения на них; построить ее структурную и математическую модели; описать ее на каком-либо формальном абстрактном языке;

определить цели, принуждающие связи, критерии действия системы.

После идентификации системы строится концептуальная модель, являющаяся «идеологической» основой будущей математической модели. Именно в ней отражается состав критериев оптимальности и ограничений, определяющих целевую направленность модели. Перевод, на этапе формализации качественных зависимостей в количественные, преобразует критерий оптимальности в целевую функцию, ограничения — в уравнения связи, концептуальную модель- в математическую модель.

Если посмотреть на схему построения математической модели (см. рис. (2.1.), то можно увидеть, что процесс ее построения представляет собой не только прямую, но и обратную связь отдельных этапов. Это означает, что при работе над последующим этапом приходится возвращаться к предыдущим для уточнения тех или иных моментов.

Рис.(2.3.) Факторная модель производственной системы очистки воды.