Файл: Математическое моделирование в экологии.doc

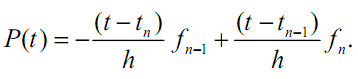
Интегрируя этот полином от t_n до t_{n - 1}, получаем следующий метод:

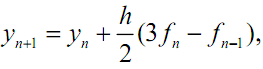(3.15)

который является двухшаговым, поскольку использует информацию в двух точках - t_n и t_{n - 1}. Аналогично, если N = 2 , то P есть квадратичный полином, интерполирующий данные (t_n-2 , f_n-2 ), (t_n-1 , f_n-1), (t_n , f_n), а соответствующий метод имеет вид

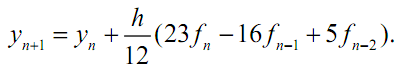(3.16)

Если N = 3, то интерполяционный полином является кубическим, а соответствующий метод определяется формулой

(3.17)

Отметим, что метод (3.16) является трехшаговым, а (3.17) – четырехшаговым. Формулы (3.15) – (3.17) известны как методы Адамса –Башфорта. Метод (3.15) имеет второй порядок точности, поэтому его называют методом Адамса – Башфорта второго порядка. Аналогично, методы (3.16) и (3.17) называют соответственно методами Адамса – Башфорта третьего и четвертого порядков.

Этот процесс, в принципе, можно бы продолжить, используя все большее число предыдущих точек, а следовательно, и интерполяционный полином P более высокой степени, и получить Адамса – Башфорта сколь угодно высокого порядка. Однако точность вычислений с увеличением порядка возрастает нелинейно. Чем дальше отстоит предыдущая точка от текущей точки, тем слабее она влияет на точность. Многошаговые методы порождают проблему, которая не возникала при использовании одношаговых методов. Так как в

рассматриваемых методах используется информация о нескольких ранее полученных точках, то в отличие от одношаговых методов они не обладают свойством "самостартования". Поэтому прежде чем применять многошаговый метод, приходится вычислять исходные данные с помощью какого-либо одношагового метода. Часто для этого прибегают к методу Рунге - Кутта.

11.3.9. Методы прогноза и коррекции

Методы Адамса – Башфорта используют уже сосчитанное значение в точке n, t и в предыдущих точках. В принципе, при построении интерполяционного полинома мы можем использовать и точки t_n+1, t_n+2 и т.д. Простейший случай при этом состоит в использовании точек t_n+1, t_n ,…, t_n-N и построении интерполяционного полинома степени N +1. При этом возникает класс методов, известный как методы Адамса - Моултона. Если N = 0, то P - линейная функция, проходящая через точки (t_n , f_n) и (t_n+1 , f_n+1), и соответствующий метод

(3.18)

является методом Адамса - Моултона второго порядка.

Если, N = 2 , то P - кубический полином, построенный по точкам (t_n+1, f_n+1), (t_n, f_n), (t_n-1, f_n-1) и (t_n-2, f_n-2) и соответствующий метод

(3.19)

является методом Адамса-Моултона четвёртого порядка.

Заметим, что в формулах (3.18) и (3.19) значение f_n+1 неизвестно. Дело в том, что для вычисления f(t_n+1, y_n+1)=f_n+1 нужно знать три значения y_n+1, которое само пока является неизвестным. Например, соотношение (3.18) является уравнением

(3.20)

относительно неизвестного значения y_n+1. То же самое справедливо и относительно (3.19). Следовательно, методы Адамса-Моултона определяют y_n+1 неявно и в силу этого называются неявными. В то же время, методы Адамса – Башфорта называются явными, поскольку они для нахождения значения y_n+1 не требуют решения никаких уравнений. На практике обычно не решают уравнение (3.20), а используют совместно явную и неявную формулы, что приводит к методу прогноза и коррекции. Одним из широко используемых методов прогноза и коррекции является объединение методов Адамса четвёртого порядка (3.17) и (3.19):

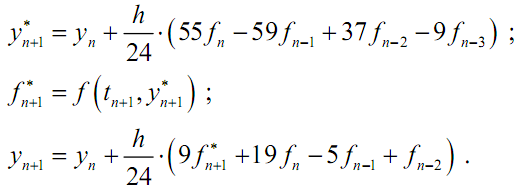
В целом этот метод является явным. Сначала по формуле Адамса – Башфорта вычисляется значение , являющееся «прогнозом» для . Затем используется для вычисления приближенного значения , которое, в свою очередь, используется в формуле Адамса - Моултона. Таким образом, формула Адамса -Моултона «корректирует» приближение, даваемое формулой Адамса– Башфорта.

Может возникнуть вопрос - зачем вообще нужна коррекция, если прогноз имеет четвёртый порядок точности? Ответ на этот вопрос дает оценка величины членов, выражающих погрешность. Ошибка усечения ряда для формулы прогноза (3.17) равна:

а для формулы коррекции (3.19):

т. е. погрешность усечения ряда при коррекции в 13 раз меньше.

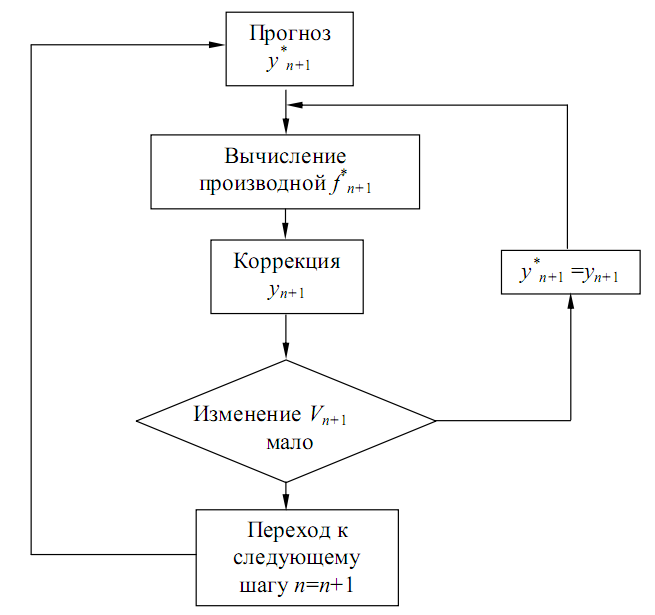
Рис. 3.5. Алгоритм метода прогноза и коррекции

Формулы коррекции гораздо более точны, чем формулы прогноза, а потому их использование оправданно, хотя и связано с дополнительными вычислениями (рис. 3.5). Чтобы добиться наибольшей точности вычисления, коррекцию в методах прогноза и коррекции часто повторяют на одном и том же шаге несколько раз. На практике для обеспечения сходимости решения достаточно 2-3 циклов коррекции.

11.3.10. Краткая характеристика методов прогноза и коррекции.

По сравнению с одношаговыми методами, методы прогноза и коррекции имеют ряд особенностей:

1) Для реализации методов прогноза и коррекции необходимо иметь информацию о нескольких предыдущих точках. Поэтому они не относятся к числу «самостартующихся» методов и начинать решение приходится с помощью какого-либо одношагового метода. По этой же причине в процессе решения дифференциальных уравнений нельзя изменять шаг интегрирования.

2) Одношаговые методы и методы прогноза и коррекции обеспечивают приблизительно одинаковую точность результатов, однако вторые в отличие от первых позволяют легко оценить погрешность на шаге.

3) Применяя метод Рунге - Кутта четвёртого порядка, на каждом шаге приходится вычислять четыре значения функции, в то время как для обеспечения сходимости метода прогноза и коррекции того же порядка точности достаточно двух значений функции. Поэтому методы прогноза и коррекции требуют почти вдвое меньше машинного времени, чем методы Рунге - Кутта сравнимой точности.

11.3.11. Выбор шага и погрешность решения.

Одним из важнейших практических вопросов, которые встают перед инженером, составляющим программы решения дифференциальных уравнений, является выбор подходящей величины шага. Если шаг слишком мал, то расчёт потребует неоправданно много машинного времени, а число ошибок на

отдельных шагах, складывающихся в суммарную ошибку, будет весьма велико. Если же наоборот - шаг выбран слишком большим, то значительной будет погрешность, обусловленная усечением рядов, и накопившаяся суммарная ошибка будет также недопустимо большой (рис.3.6).

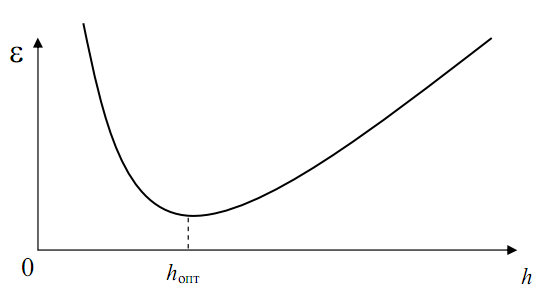
Рис. 3.6. Выбор оптимального шага интегрирования

Кроме того, при больших значениях h возникает опасность появления цифровой неустойчивости решения. Важно различать между собой две меры погрешностей дискретизации [9],[10]:

а) локальная ошибка - это погрешность, вносимая в вычислительный процесс на каждом шаге вычислений.

б) глобальная ошибка - это разность между вычисленным и точным значениями величины на всем этапе реализации численного алгоритма, определяющая суммарную погрешность, накопившуюся с момента начала вычислений. Обычно, выбирая величину шага, стремятся, чтобы локальная ошибка на шаге была меньше некоторой заданной допустимой величины. Вообще говоря, если порядок точности метода Р, то локальная ошибка определяется выражением:

L(h) = c h^p+1,

где c - некоторая постоянная; h - шаг интегрирования.

Указанное выражение с помощью θ-символики может быть записано более компактно:

L(h) = θ (hp+1).

Например, рассмотрим метод Эйлера:

Отсюда заключаем, что для метода Эйлера p =1, т.е. метод имеет первый порядок точности, а локальная ошибка определяется формулой:

L(h) = θ (h2 ).

Рассмотрим теперь глобальную ошибку дискретизации в конечной точке t=t_N. По мере повышения требований к точности, длина шага h будет убывать, а общее из числа N, необходимое для достижения t_N, будет возрастать: