ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1175
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
Далее, глобальная ошибка E(h) может быть представлена как сумма N локальных ошибок и поэтому мы можем, округляя, записать:
E(h) = N θ(hp+1) = θ(hp ).
Для метода Эйлера p =1, так что уменьшение длины шага в 2 раза уменьшает среднюю локальную ошибку примерно в 2p+1 = 4 раза. Но так как для достижения tN теперь потребуется вдвое больше шагов, то глобальная ошибка ум-еньшится лишь в 2p = 2 раза. Если используется один из методов прогноза и коррекции, то ошибка на шаге определяется величиной последнего члена в формуле коррекции. При использовании же одношаговых методов Рунге-Ку-тта, локальную ошибку не удается выразить в явной форме. Один из методов оценки этой ошибки основан на двойном счете. Если для вычисления значения искомой функции yn+1 в точке tn+1 используется шаг h, то разность между истинным и вычисленным значениями на данном шаге равна:
![]()
Если уменьшим шаг
вдвое и выполнив два шага вычислим
![]() в точке tn+1,
то получим:
в точке tn+1,
то получим:
![]() (3.21)
(3.21)
Вычитая это выражение из предыдущего, найдем:
![]()
Отсюда можно найти локальную погрешность:
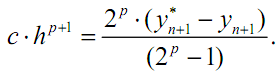 (3.22)
(3.22)
Данная формула называется правилом Рунге. Если ошибка на данном шаге слишком велика, то шаг делят пополам и вычисления повторяют вновь.
Запишем формулу (3.22) в виде:
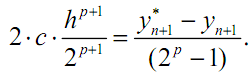
Подставляя полученное выражение в (3.21) и полагая p=4, найдём приближенное значение ошибки на одном шаге:
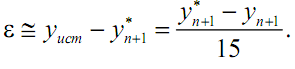 (3.23)
(3.23)
Из (3.23) вытекает уточнённое решение:
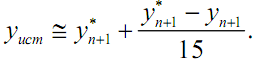
Недостатком этого метода является то, что значение yn+1 приходится вычислять дважды, причем второй раз с помощью двух шагов. Тем не менее, эта процедура часто включается в вычислительный алгоритм для автоматического изменения шага в процессе вычислений и часто используется в методах Рунге - Кутта. Главное достоинство методов Рунге - Кутта - простота начала счета и возможность изменения величины шага в процессе вычисления. С
другой стороны, главным достоинством методов прогноза и коррекции является простота оценки ошибки на шаге.
11.3.12. Жесткие задачи
Некоторые обыкновенные дифференциальные уравнения (ДУ) не решаются ни одним из рассмотренных методов. Чтобы понять, почему это так, рассмотрим структуру ДУ. В общем случае ДУ n-го порядка имеют n постоянных времени. Если одна из постоянных времени достаточно мала по сравнению с шагом интегрирования, то задача называется жесткой и ее трудно решить обычными методами. В таких случаях шаг должен быть достаточно мал, чтобы можно было учитывать изменения наиболее быстроизменяющихся членов уравнения. В противном случае решение становится неустойчивым. Если величина шага очень мала по сравнению с интервалом, на котором отыскивается решение, то для получения решения потребуется очень много времени. А накапливающиеся в процессе длительных вычислений погрешности округления могут привести к получению бессмысленного результата. Рассмотрим, например, систему:
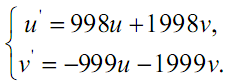
Если u(0) = v(0) =1, то решением будут (рис.3.7):
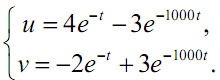
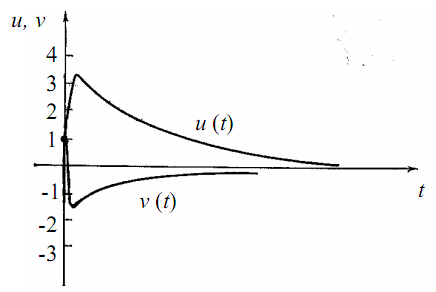
Рис. 3.7. Решение системы уравнений
После очень небольшого промежутка времени решение весьма близко к фун-кциям:
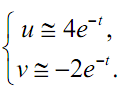
Предположим, что мы должны решить эту систему посредством метода Эйлера. Дискретное решение можно записать формулой:
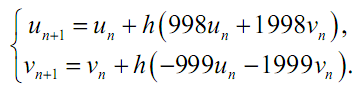
где u0= v0=1.
Если выбрать h = 0,02, то:
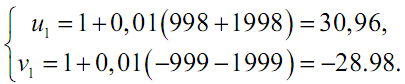
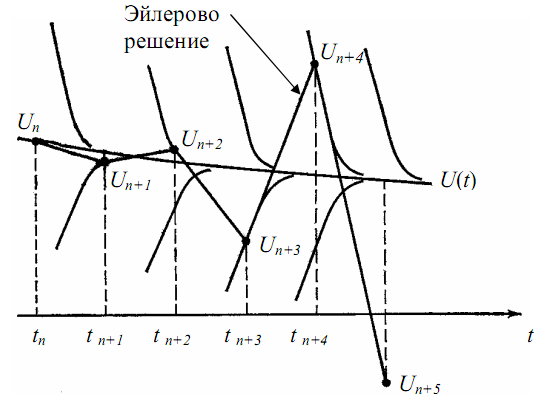
Рис.3.8. Семейство решений
Если сделать еще несколько шагов интегрирования, то результаты примут катастрофический характер. Это явление можно представить себе визуально, рассматривая семейство решений ассоциированных с u(t) (рис.3.8).
Переходная часть решения, которая, казалось бы, давно уже практически исчезла, тем не менее, мешает увеличить длину шага. Это особенно досадно, потому что на данном этапе вычислений решение очень гладко и, казалось бы, можно увеличить шаг.
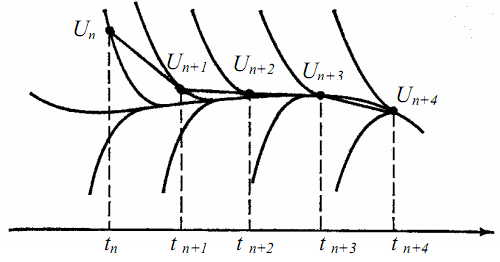
Рис.3.9. Работа неявного метода Эйлера
Большинство стандартных методов не приспособлено для решения жестких уравнений. Поэтому были изобретены специальные методы. Простейшим из них является так называемый неявный метод Эйлера, выражаемый формулой:
![]()
Работу неявного метода Эйлера покажем графически (рис.3.9).
Разработка эффективных методов для жестких уравнений является областью активных исследований.
назад
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
Термин «имитация» (simulation) появляется в США в начале 60 гг. в связи с изучением сложных систем, траектории движения которых зависят от многих параметров или функций. Позднее это понятие стали использовать в более широком смысле. Любое воспроизведение в машине сложного динамического процесса с последующим анализом множества вариантов его течения, стали называть имитацией [14]. Исследуемый объект при имитационном моделировании представляют в виде конечной суммы элементарных звеньев, параметры которых находятся по экспериментальным или теоретическим данным. Имитационная математическая модель позволяет воспроизвести в ЭВМ физические процессы, которые описываются теми же ДУ, что и процессы, протекающие в исследуемом объекте или системе. Благодаря этому можно изучить свойства объекта еще до того, как он будет построен, или исследовать его работу в особых, имеющих определенное значение, режимах.
Имитационное моделирование на ЭВМ динамических систем целесообразно использовать в тех случаях, когда последние описываются линейными ДУ высоких порядков и их аналитическое исследование затруднено, а так же при исследовании нелинейных систем и систем с переменными параметрами, для которых аналитические методы часто вообще отсутствуют.
11.4.2. Объекты моделирования
Объекты моделирования рассматриваются нами как сложные технические системы, состоящие из совокупности взаимодействующих элементов. Они могут включать в себя электрические, механические, гидравлические, пневматические, электронные и другие компоненты.
Их функционирование описывается переменными, связанными с механическими и электромагнитными явлениями, свойствами движущихся жидкостей и газов и т. д. Такие системы называют динамическими системами. Математическая модель динамической системы представляет собой систему обыкновенных ДУ, которая в нормальной форме Коши имеет вид:
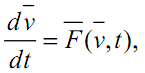
где
![]() -
вектор фазовых
координат; t
- независимая переменная (время).
-
вектор фазовых
координат; t
- независимая переменная (время).
Задача моделирования таких объектов состоит в определении оптимальных параметров и структуры исходя из заданного описания внешней среды и технических требований к объекту.
11.4.3. Динамическая модель исследуемого объекта
Построение математической модели объекта осуществляется на основе его динамической модели. Динамическая модель - это абстрактное графическое отображение основных физических свойств объекта и характеристик его взаимодействия с внешней средой [13].
При построении динамической модели следует принимать во внимание лишь те физические свойства объекта и воздействия внешней среды, которые могут оказать существенное влияние на точность результатов моделирования. Такой подход позволит избежать необоснованной избыточности в его математическом описании.
Структура динамической модели представляется в виде совокупности взаимодействующих элементов и её сложность зависит от степени абстрагирования при отображении физических свойств объекта. При построении динамических моделей используют следующие методы:
- методы сеток;
- метод функционально законченных элементов;
- метод сосредоточенных масс.
Методы сеток подразделяют на метод конечных разностей и метод конечных элементов. Они обычно используются при построении алгоритмической модели на микроуровне в системах с распределенными параметрами, описываемыми дифференциальными уравнениями в частных производных.
Метод функционально законченных элементов основан на выделении типовых элементов системного объекта, завершенных в конструктивном отношении и предназначенных для выполнения определенных функций (например, в гидромеханической системе - участок гидромагистрали, золотниковый клапан, дроссель, обратный клапан, насос, гидромотор и т. д.) Имея библиотеку математических моделей функционально законченных элементов и зная структуру технического объекта, можно составить полную математическую модель.