Файл: Математическое моделирование в экологии.doc

Рис. 4.18 Двигатель постоянного тока

Рассмотрим отдельно электрическую и механическую части электрического двигателя. Входной величиной здесь является напряжение, а выходной - частота вращения вала двигателя ω. Под влиянием напряжения, через обмотку якоря протекает ток i, который, взаимодействуя с магнитным полем возбуждения Ф, создает на валу электродвигателя движущий момент:

M = c × i , (4.1)

где с - коэффициент, зависящий от конструкции двигателя.

При вращении якоря в магнитном поле в нем возникает ЭДС:

e = c × i. (4.2)

Она направлена против питающего напряжения U и поэтому вызывает уме-ньшение тока i. Коэффициент пропорциональности С в формулах (4.1) и (4.2) зависит от конструкции двигателя и силы магнитного поля Ф. Рассмотрим схему замещения якорной цепи двигателя при индуктивности якоря L_я = 0 (рис.4.19). Внешнее напряжение U уравновешивается суммой падения напряжения UR на омическом сопротивлении R якоря U и ЭДС e.

Следовательно, можно записать: U - e =U_R.

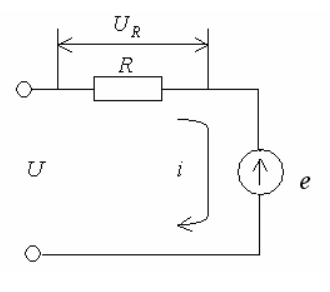
Рис. 4.19. Схема замещения

Зная величину U_R, можно определить ток i, а ток i определяет момент M на валу двигателя, последний, в свою очередь, связан с частотой вращения урав-нением движения:

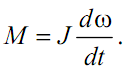(4.3)

Определив ω - найдем ЭДС е. Рассмотренную причинно-следственную связь физических величин представим сетью связей (рис.4.20).

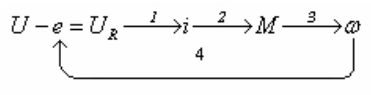
Рис. 4.20

В соответствии с сетью связей, запишем физические зависимости и следующие из них передаточные функции:

Сопоставив полученные выражения для передаточных функций с сетью связей, легко построить структурную схему двигателя (рис.21).

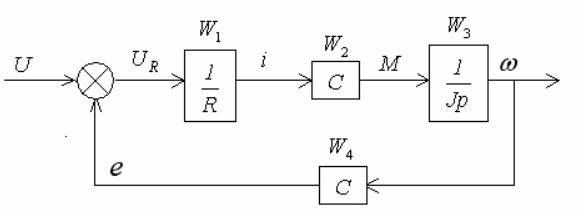
Рис.4.21. Структурная схема двигателя

Пример 4.3

Рассмотрим регулируемый электропривод на основе двигателя постоянного тока. Требуется построить имитационную модель электропривода с учетом массы якоря электропривода. Индуктивностью якорной цепи электродвигателя пренебречь (рис.4.22).

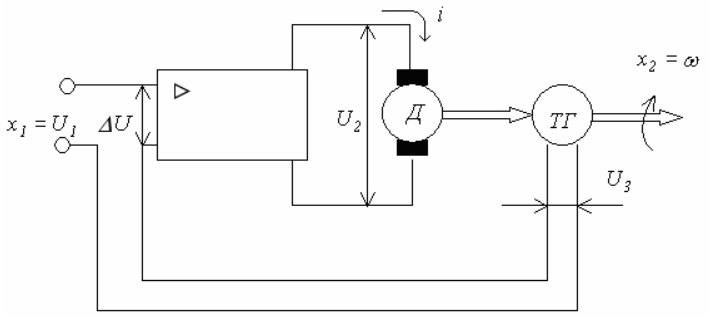
Рис. 4.22. Регулируемый электропривод

В данной системе входное воздействие – напряжение U₁- сравнивается с выходным напряжением тахогенератора (ТГ) U₃. Разница этих напряжений ΔU =U₁ -U₃ усиливается усилителем Y, и подается на якорь двигателя постоянного тока Д. Частота вращения вала электродвигателя с помощью тахогенератора ТГ, преобразуется в пропорциональный сигнал обратной связи U3. Сеть связей рассматриваемой системы имеет следующий вид (рис. 4.23).

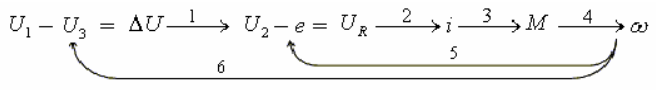
Рис.4.23. Сеть связей

где U₂- напряжение на якоре; e – ЭДС якоря; U_R – падение напряжения на сопротивлении якоря; R - сопротивление якоря; i - ток якоря; M - момент на валу; J - момент инерции якоря; ω - частота вращения; c - постоянный коэффициент; U₃- напряжение тахогенератора; k_ТГ - коэффициент передачи тахогенератора. Структурная схема представлена на рис.4.24.

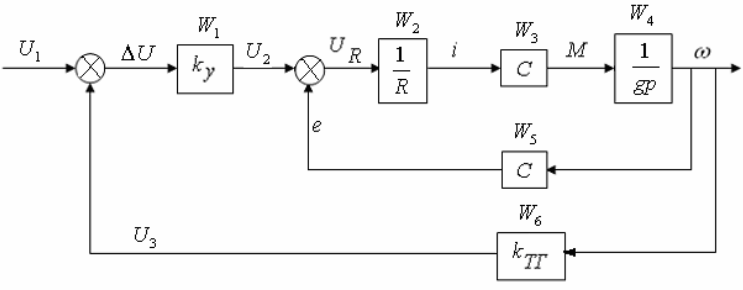
Рис.4.24. Структурная схема

11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши

1) Интегрирующее звено.

Из передаточной функции интегрирующего звена

следует искомое дифференциальное уравнение:

Эквивалентная структурная схема (рис.4.25) состоит из последовательно соединенных элементарных звеньев с передаточными функциями k_i и 1/p

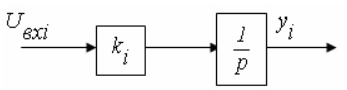
Рис.4.25. Структурная схема

2) Апериодическое звено.

Передаточная функция звена:

откуда

или

Полученному дифференциальному уравнению соответствует эквивалентная структурная схема на рис.4.26.

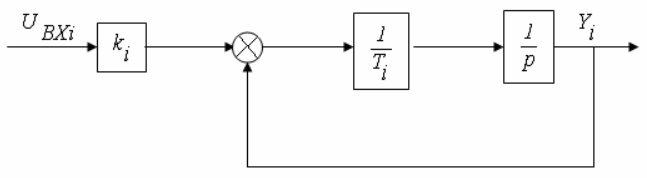
Рис.4.26. Структурная схема

3) Колебательное звено.

Колебательное звено описывается дифференциальным уравнением второго порядка, которому равносильна система из двух уравнений первого порядка. Преобразовывая выражение для передаточной функции звена

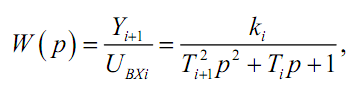
получаем

Введем обозначение pY_{i +1} = Y_i в последнее уравнение. Получим:

Система дифференциальных уравнений в форме Коши для колебательного звена имеет вид:

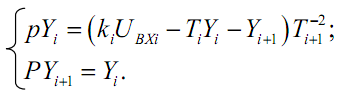
Эквивалентная структурная схема этого звена изображена на рис.4.27.

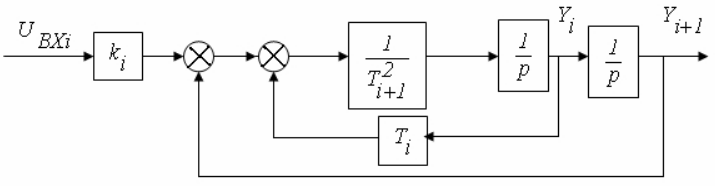
Рис. 4.27. Структурная схема

4) Дифференцирующее звено с замедлением.

Запишем передаточную функцию звена в виде

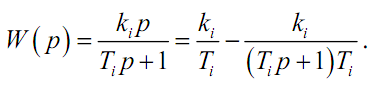
Эквивалентная структурная схема (рис.4.28) включает элементарное усилительное звено с передаточной функцией k_i /T_i и рассматривавшееся выше апериодическое звено. Таким образом, для описания дифференцирующего звена с замедлением можно использовать уравнение для апериодического звена путем вычитания сигнала Y_i из сигнала .

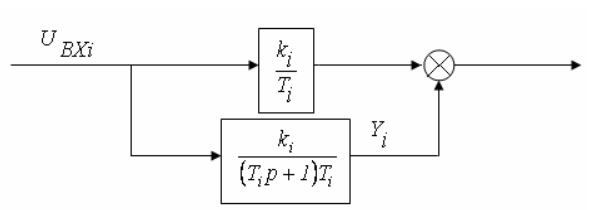
Рис. 4.28. Структурная схема

5) Сложное звено.

В структурной схеме исследуемой динамической системы может встретиться сложное звено с передаточной функцией

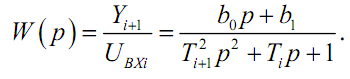
Такое звено можно описать с помощью двух дифференциальных уравнений первого порядка. Чтобы их получить, выполним с передаточной функцией следующие преобразования:

Введя обозначение , перепишем последнее уравнение в виде:

Раскроем скобки.

Упростив, получаем дифференциальные уравнения первого порядка в форме Коши.

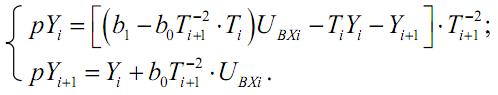
С целью сокращения записи представим эти уравнения в виде:

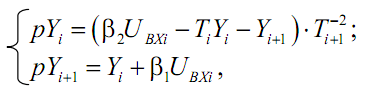
где .

На рис. 4.29 дана эквивалентная структурная схема рассмотренного звена.

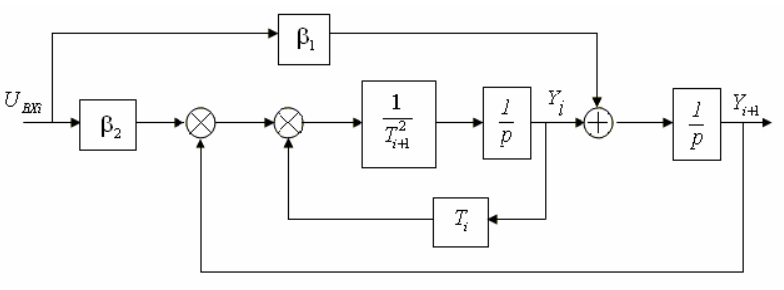
Рис. 4.29. Структурная схема

Если степень полинома в числителе передаточной функции элемента равна степени полинома в её знаменателе, то необходимо на структурной схеме системы представить этот элемент как параллельное соединение двух эле-ментов в соответствии со следующими формулами:

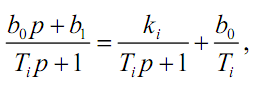
где ;

где .

Если степень полинома в числителе передаточной функции элемента равна степени полинома в её знаменателе, причем знаменатель имеет действительные корни, то знаменатель можно разложить на сомножители. Тогда на структурной схеме системы можно представить этот элемент как параллельное соединение двух элементов в соответствии со следующей схемой:

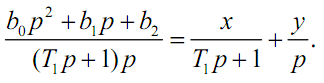
Требуется найти неизвестные коэффициенты, обозначенные как x и y . Преобразуем последнее уравнение.

(4.4)

При p = 0 y = b₂. (4.5)

Решая уравнения (4.4) и (4.5) совместно, определяем другой неизвестный коэффициент x .

Рассмотрим второй пример.

откуда

(4.6)

При p = 0 x + y = b₂. (4.7)

Решаем уравнения (4.6) и (4.7) совместно. Получаем:

Если степень полинома в числителе передаточной функции элемента больше степени полинома в её знаменателе, то этот элемент следует объединить с одним или несколькими другими элементами структурной схемы с целью получения результирующей передаточной функции, у которой степень полинома в числителе не превышает степень полинома в знаменателе.

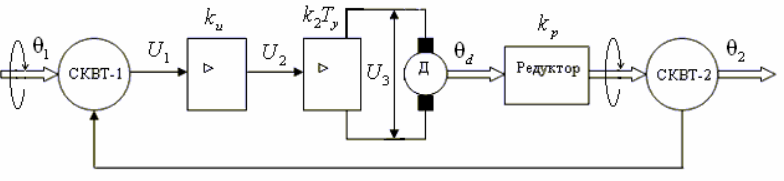
Рис. 4.30 Функциональная схема