Файл: Математическое моделирование в экологии.doc

Параметрами упругих и диссипативных элементов являются соответственно теплоемкость C_Tи коэффициент теплового сопротивления µ_T. Потенциальная переменная Т_ухарактеризует температуру дискретного элемента, а Т_д- представляет собой разность температур смежных дискретных элементов.

Топологические уравнения имеют вид:

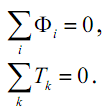
Первое уравнение выражает условие равновесия потенциалов на поверхностях контакта дискретных элементов. А второе – условие непрерывности функции температуры.

11.6.1. Сущность метода электроаналогий.

С появлением электротехники в ней стали широко применяться электрические схемы в качестве наглядных образов исследуемых объектов. Электрические схемы глубоко изучены. В отличие от механической энергии электрическая энергия передается в электрических цепях посредством ветвей, содержащих резисторы,

конденсаторы, катушки индуктивности и др., а перераспределяется электрическая энергия между ветвями посредством узлов. Поэтому электрические процессы можно исследовать с помощью известных понятий: электрического тока, напряжения, э.д.с. Математическое описание электрических процессов часто совпадает с описанием процессов в объектах иной физической природы, что позволяет исследования явлений в неэлектрических системах заменить исследованиями аналогичных явлений в электрических цепях [5].

Современные сложные машины и механизмы представляют собой совокупность взаимодействующих механических, гидравлических, пневматических, электрических и других компонентов. Их динамические характеристики описываются

уравнениями, которые связаны с механическими и электромагнитными явлениями, свойствами движущихся жидкостей и газов, распространением магнитных и тепловых потоков и т.д.

Сравнивая компонентные уравнения различных видов систем, легко обнаружить их динамические аналогии (табл. 6.1). Топологические уравнения этих систем также абсолютно аналогичны. В этом проявляется единство физических законов,

применимых к разнообразным формам существования материи. Аналогия систем различной физической природы также видна, если сравнить единицы измерений потенциальных и потоковых переменных (табл. 6.2).

Метод электроаналогий не сводится к простой замене законов механики законами электротехники. Такая замена в общем случае невозможна. Например, чтобы построить электромеханическую модель движения твердого тела вокруг неподвижной точки, необходимо рассматривать векторную функцию изменения момента

количества движения и тензор инерции, определяющие динамику твердого тела. Законы электрических цепей выражаются скалярными функциями и не могут полностью заменить законы теоретической механики.

Таблица 6.1

Компонентные уравнения

Таблица 6.2

Единицы физических переменных

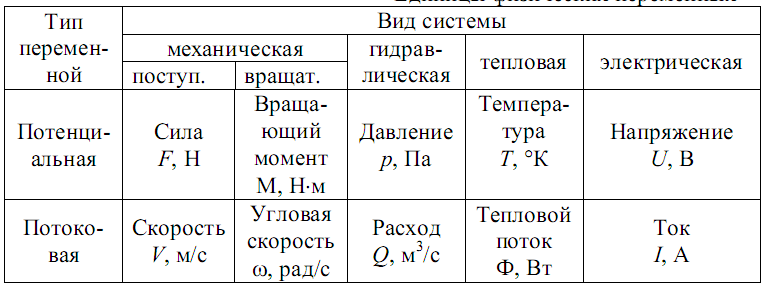
Концепция метода электроаналогий основана на том, что этот метод добавляет к законам теоретической механики законы электротехники. Это позволяет расширить представление о происходящих явлениях и формализовать синтез математических моделей сложных механических систем. Отметим основные аспекты

данной концепции.

Первый аспект – возможность применения для решения задач законов Кирхгофа из электротехники. Они дают электрическим моделям значительное преимущество перед моделями иной физической природы, так как в других областях техники нет законов, полностью адекватных законам Кирхгофа. Это замечание, прежде всего, относится к механическим объектам, которые обычно представляют в виде структурно-кинематических схем. Кинематическая схема характеризует одновременно геометрию механизма и его движение, что затрудняет топологическое представление механических систем.

Наиболее сложно в механике применить аналог первого закона Кирхгофа, в соответствии с которым сумма токов в узле электрической схемы равна нулю. Продифференцировав уравнение токов в узле, получим важное следствие, вытекающее из первого закона Кирхгофа: сумма производных токов (применительно к

механике – ускорений) в узле также равна нулю. Данное утверждение в терминах механики не столь очевидно, как в электротехнике.

Второй аспект – применение в эквивалентных электрических схемах замещения идеальных трансформаторов, как с постоянными, так и с переменными коэффициентами трансформации.

Трансформатор с переменным коэффициентом трансформации (случаи плоских криволинейных и пространственных движений тел) представляет собой амплитудный модулятор напряжений, токов и производных токов. Математическое описание таких объектов уравнениями механики затруднительно.

Третьим аспектом концепции метода электроаналогий являются электрические разъемные соединения, с помощью которых эквивалентные электрические схемы замещения можно собирать из отдельных независимых модулей (подсистем), что позволяет конструировать математические модели по агрегатному (расширяемому) принципу.

Основной подход математического моделирования с использованием электромеханических аналогий сводится к следующей последовательности действий:

1) разделить механическую систему на отдельные подсистемы, каждая из которых включает одну сосредоточенную массу;

2) применяя принцип Даламбера, составить уравнения кинетостатики, определяющие движение тела с выделенной массой;

3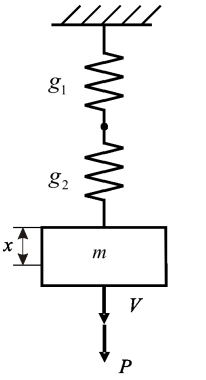)спроектировать векторные уравнения кинетостатики на координатные оси и заменить векторные соотношения скалярными;

4) используя таблицу электроаналогий (табл.6.1), выделить в механической системе инерционные, диссипативные и упругие элементы;

5) построить на основе полученных уравнений эквивалентную электрическую схему замещения;

6) на основе электрической схемы записать уравнения по первому закону Кирхгофа и уравнения трансформаторов. Продифференцировать эти уравнения и добавить к уравнениям теоретической

Рис. 6.1 Груз на двух механики.

пружинах.

Уравнения по второму закону Кирхгофа записывать не нужно, так как они совпадают с уравнениями кинетостатики для сил и моментов. Рассмотрим общий подход к синтезу имитационных моделей методом электроаналогий на простейших примерах.

Пример 6.1

Составить математическую модель груза массой m, подвешенного на двух пружинах с податливостями g₁=1/c₁ и g₂=1/c₂, где c₁и c₂- жесткости пружин (см. рис. 6.1). В соответствии с таблицей электроаналогий (Таб. 6.1 и 6.2), строим электрическую схему, эквивалентную данному механическому устройству.

Индуктивности, емкости, э.д.с., напряжения и токи в электрических схемах будем обозначать с помощью соответствующих символов, принятых в механике.

В данном механизме скорости деформаций пружин V1 и V2 складываются. Усилие на обеих пружинах F_y одинаковое. Этому условию соответствует параллельное включение конденсаторов в электрической схеме (рис. 6.2).

Уравнения Кирхгофа для этой схемы:

P - F_и - F_у = 0, (6.1)

V -V₁-V₂ = 0. (6.2)

На основании уравнений Кирхгофа строим сеть связей (рис. 6.3).

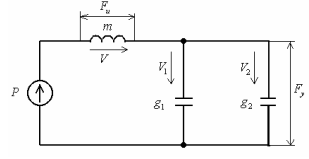
Рис. 6.2. Электрическая схема

В уравнении (6.1) выносим вправо от знака равенства инерционную составляющую F_u. От нее с помощью соотношения переходим к скорости изменения тока. Интегрируя скорость изменения тока , определяем ток V , а интегрируя ток V , получаем суммарный заряд на конденсаторах x . Заметим, что соотношение токов и напряжений для индуктивности аналогично 2-му закону Ньютона. Скорость изменения тока является аналогом ускорения, ток – аналогом скорости, а суммарный заряд на конденсаторах - аналогом суммарного перемещения груза.

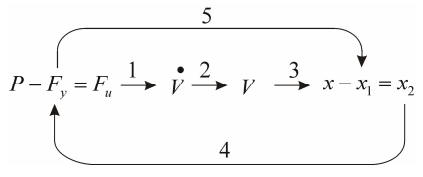
Рис. 6.3

Таблица 6.3

Передаточные функции элементарных звеньев

Проинтегрируем уравнение (6.2). В результате получаем уравнение

x - x₁ - x₂ = 0.

Это соотношение баланса зарядов на конденсаторах g₁и g₂, которое позволяет завершить построение сети связей для рассматриваемого устройства. Каждой ветви сети связей соответствует элементарное звено со своей передаточной функцией (табл. 6.3). Используя выражения передаточных функций для элементарных звеньев, переходим от сети связей к структурной схеме динамической модели (рис. 6.4).

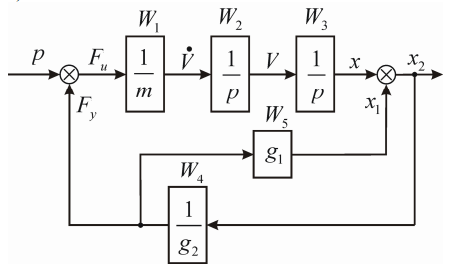
Рис. 6.4

Пример 6.2

Построить эквивалентную электрическую схему механического устройства (рис. 6.5).

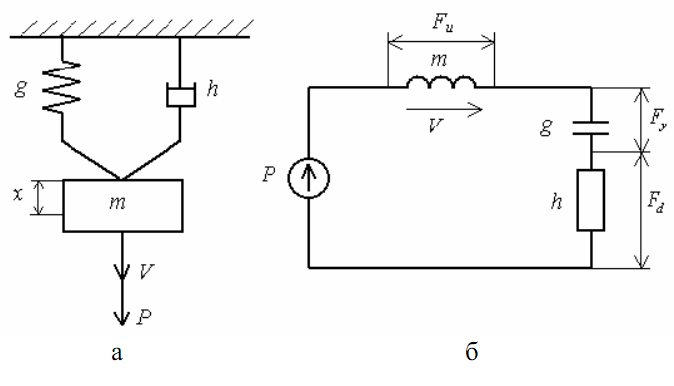
Рис. 6.5. Механическое устройство и его эквивалентная схема

В данном устройстве скорости деформаций пружины и демпфера одинаковы и равны скорости движения груза. В электрической схеме этому условию соответствует последовательное соединение индуктивности, ёмкости и сопротивления.

Записываем уравнение по второму закону Кирхгофа:

P - F_u - F_y - F_d = 0 . (6.3)

Построим сеть связей. Для этого в уравнении (6.3) выносим вправо от знака равенства инерционную составляющую F_u, с помощью уравнения определяем скорость изменения тока (ускорение) , дважды интегрируем эту переменную и вводим в систему обратные связи по диссипативной составляющей F_dи по упругой составляющей F_y(рис. 6.6).