Файл: Математическое моделирование в экологии.doc

Для перехода к новой симплекс-таблице необходимо поменять места- ми х₁ и х₄, а все элементы разрешающей строки умножаем на элемент а^*₄₁ = 1. Все элементы разрешающего столбца умножаем на -а^*₄₁=-1, кроме самого разрешающего элемента, что приведено в табл. 5.3.

Таблица 5.3

j^*

	х₁	х₂	х₃	ь_j
х₄	1	1/2	1/2	5/2
х₅	-1	3	-1/2	4
х₆	1	2	1/2	8
p_j	-3	1	3	F^*

i^*

Остальные элементы таблицы вычисляем по формуле, значение нового элемента равно:

Тогда для элемента а₅₂

Аналогично для р_j

и для b_i

Так же для F

и т.д.

Заполняем табл. 5.3. Так как все коэффициенты р_j в табл. 5.3 положительны, решение найдено. Значение F из последней строки табл. 5.3 с противоположным знаком будет решением целевой функции, т.е.

F_min = — 7.

Базисное решение: х₁ = 2,5; х₂ = 0; х₃ = 0;

x₄=0; х₅ = 6,5; х₆ = 5,5.

Проверка: F_min= -3х₁ + х₂ + 3х₃ = -3 х 5/2 = -7,5.

Лекция 11. Функциональные модели.

Функциональная зависимость может выражаться в виде алгебраических равенств или дифференциальных уравнений. Рассмотрим наиболее типичные функции, моделирующие те или иные экологические процессы.

Функции роста чаще всего обозначают некоторую аналитическую зависимость между ростом параметра, например массы вещества, и факторами, обусловливающими этот рост. Так, если рас- сматривать прирост сухого вещества растения W в зависимости от прироста субстрата S за период времени dt, то получим уравнение роста

Далее темп роста (при условии, что система не получает из внешней среды и не теряет никакого материала) можно предста- вить в виде функции

Если принять допущения, что количество энергии роста пропорционально сухой массе W; механизм роста имеет максимальный темп на протяжении всего времени, пока существует питательная среда; процесс роста необратим и прекращается, как только истощается питательная среда, то

где μ — удельный (относительный) темп роста.

Параметр μ , зависит от вида сухой массы W соответствую- щей ресурсу питательной среды, и от скорости, с которой работает механизм роста. Интегрируя выражение (5.9), получим:

W= W₀е^?t, при 0 < t< t_f,

W=W_f, при t>t_f.

Когда W = W_f, S = 0, то W_f = W₀ + S₀ и рост внезапно прекращается, тогда

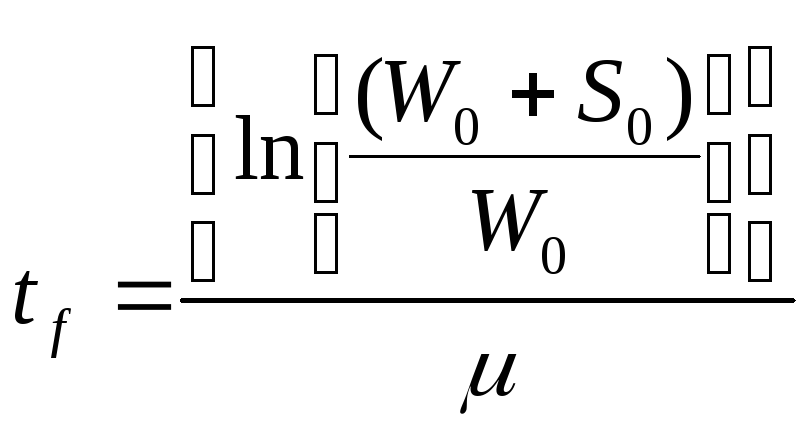
(здесь приводится результат подстановки W_f = W₀ + S₀ и t = t_f ).

Простой экспоненциальный рост, ограниченный реальным ресурсом питательной среды, графически представлен на рис. 11.2.

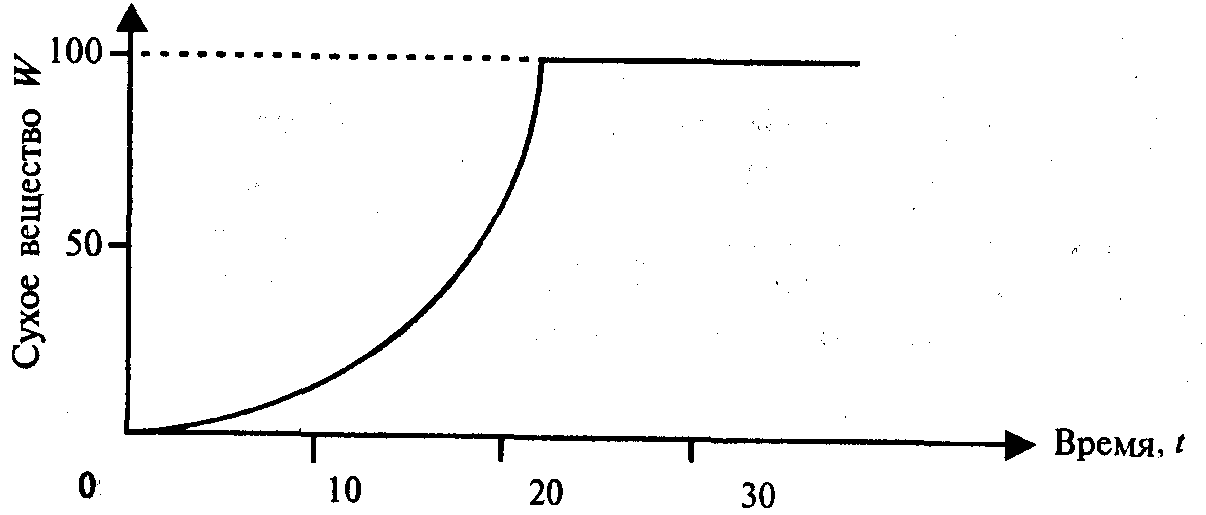
Рис. 11.2. Экспоненциальный рост с резкой отсечкой

Если предположить, что механизм роста работает со скоростью, пропорциональной ресурсу питательной среды S, то можно записать:

где k — некоторая постоянная величина.

Тогда при S= W_f — W, получим:

Интегрируя

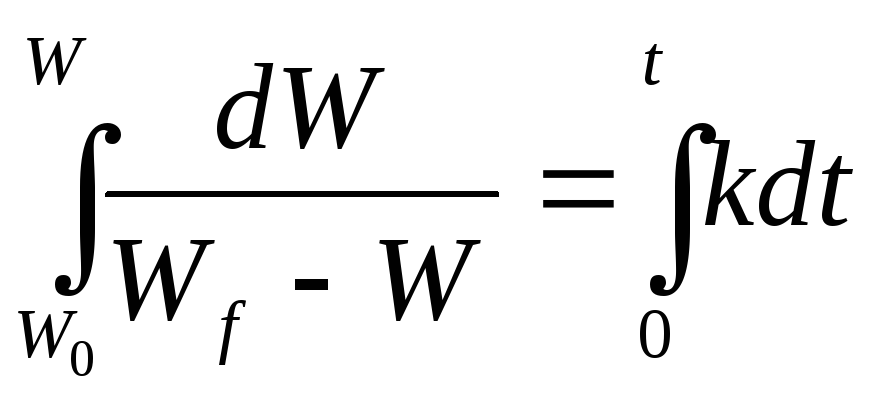
получим

. (11.10)(5.10)

При W₀ = 0

W = W_f(1 — е^-^kt).

Зависимость 11.10(5.10) графически представлена на рис. 11.3. Она представляет собой мономолекулярный рост: уравнение описывает ход простой необратимой химической реакции первого порядка.

Рис. 11.3. Мономолекулярный рост

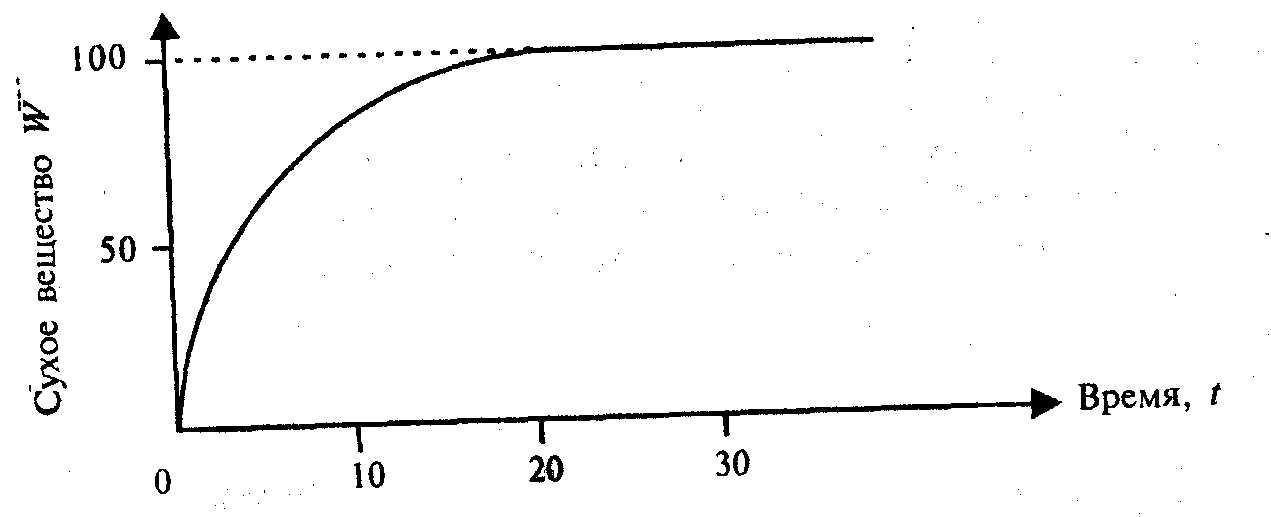
Далее можно показать, что уравнения роста могут быть:

• логистические

• Гомперца

где D — дополнительный параметр, характеризующий уменьшение μ;

• Ф. Ричардса

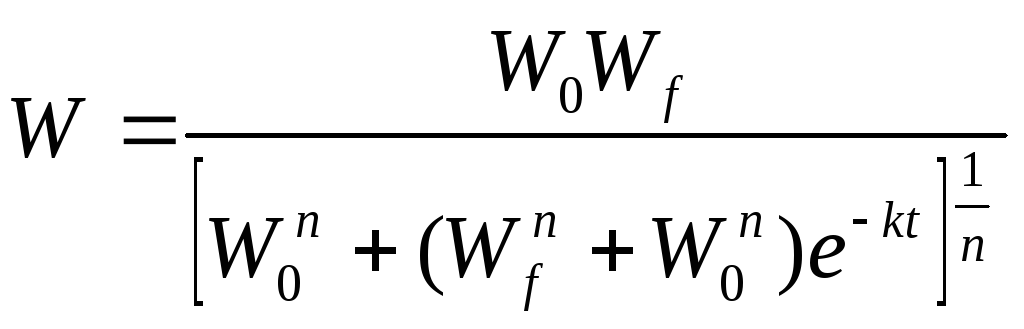
где n — параметр, n ≥ - 1;

• Л. Чантера

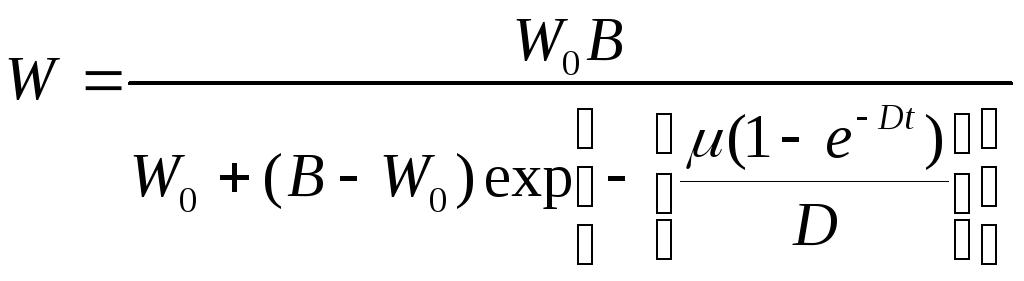
где В и D — постоянные величины.

Д. Хаксли впервые была описана аллометрическая зависимость для описания роста животных и частей их организма, а затем В. Перселлом эта зависимость была использована для описания роста растений.

Предположим, что P и Q — некоторые свойства организма (на- блюдаемые количественные характеристики): например P и Q, мо- гут быть массами различных частей животного или Р может зада- вать сухую массу растения, а Q — площадь поверхности его листь- ев. Поскольку организм растет и развивается, то P и Q будут изменяться с течением времени, т.е.

Р≡ P(t); Q ≡ Q(t).

Считается, что Р и Q аллометрически зависимы, если они удов- летворяют аллометрическому уравнению

р =аQ^b (11.10)(5.11)

где а и b — постоянные коэффициенты.

P и Q изменяются во времени таким образом, что уравнение (11.10)(5.11) сохраняет справедливость во всем интервале наблюдений.

При и можнозаписать

Q= сР^d.

Логарифмируя (5.11), получим:

ln P = lnа + blnQ

и, дифференцируя по времени

Таким образом, пропорциональные темпы роста зависят от постоянного фактора b. Аллометрическое уравнение нашло применение во многих задачах. Так, в форме

W₁=

оно описывает отношение сухой массы корней к сухой массе побегов в растущем растении. Многие модели роста могут быть представлены в форме

где W — масса;

t - время;

Р — множество параметров или постоянных коэффициентов, характеризующих организм;

Е_m — параметры или переменные, характеризующие те условия окружающей среды, которые поддаются управлению;

Е_W — показатели погоды.

Во многих случаях в экологии могут быть использованы модели «хищник — жертва». Впервые эти вопросы были затронуты в работах А. Лотки и В. Вольтера.

Пусть для данной естественной среды у обозначает число жертв, а х — число хищников. Согласно Вольтеру, имеет место:

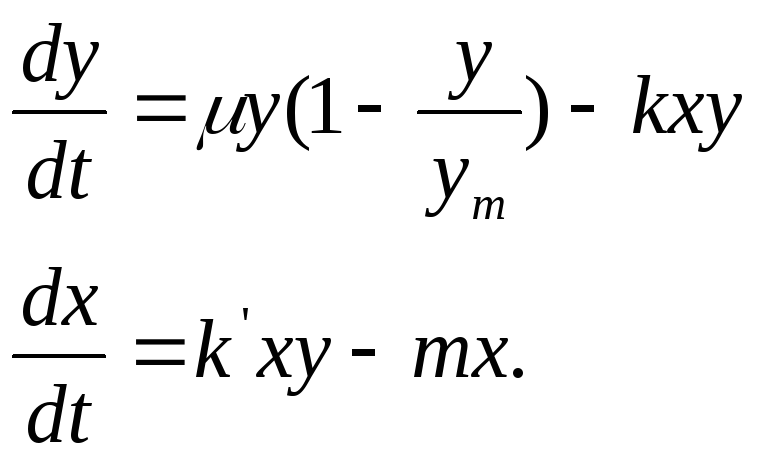(11.12)(5.12)