Файл: Математическое моделирование в экологии.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 31.03.2024

Просмотров: 1149

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Конспект лекций

Владикавказ

Математическое моделирование элементов сложных экологических систем

Лекция 1. Введение в моделирование. Исторический экскурс.

1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии

Лекция 2.

2.1. Элементы моделирования

2.2. Этапы построения математической модели

1.4. Элементы теории подобия, применяемые в моделировании

Лекция 3

3.2. Экологические модели

3.2.1. Основы экологометрики

3.2.2. Выборочный метод в экологометрике.

Зависимость числа интервалов от объема выборки

Статистический ряд по интервалам

Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам

4.4. Статистические оценки гипотез об экологических моделях

Определение вариантов выборок

Выборка из генеральной совокупности

Статистическая таблица

Лекция 5.

Результаты эксперимента

Статистическая таблица эксперимента

Пример преобразования членов уравнения регрессии

Вычисление данных для линеаризации уравнения регрессии

Нормальные уравнения мнк для некоторых функций

Статистическое оценивание уравнения регрессии и парной корреляции.

Обработка результатов наблюдений

Лекция 6.

Рекомендации по выбору вида функции

3.4. Динамические статистические модели

Посадка леса

Данные по объему сброса качественных сточных вод

Данные по объему сброса сточных вод за 5-летие

Пример расчета 5-летних средних

Условное обозначение времени

Расчетные значения для определения уравнения динамики

Ряд динамики для определения сезонных колебаний

Лекция 7. Многофакторные эколого-математические модели. Анализ влияния отдельных факторов в экологической модели.

Эксперименталъный материал исследования

Результаты проведенных опытов

8.1. Анализ влияния отдельных факторов в экологической модели.

Лекция 9. Методы оптимизации. Метод Лагранжа

Лекция 10. Метод линейного программирования.

Лекция 11. Функциональные модели.

Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.

Численные ошибки использованных для вычисления данных

Лекция 13. Статистические модели динамики.

Лекция 14. Балансовые модели.

Лекция 15.

Лекция 16. Информационные технологии в экологии. Экологические информационные системы.

1 6.1. Экологические информационные системы

1. Какова область значения для числовых характеристик?

Лекция 17. Использование информационных технологий для решения задач экологии.

Специальные приложения.

Значение функции

Значение критерия

Значение критерия

Критические значения коэффициента корреляции rk;α

2. Основы теории подобия

2.1. Подобие физических явлений и его признаки

2.2. Анализ размерностей

2.3. Первая теорема подобия

2.4. Применение методов подобия в математическом

11.3. Численные методы решения дифференциальных уравнений

11.3.1. Постановка задачи

11.3.2. Процесс численного решения

11.3.3. Метод Эйлера

11.3.4. Модифицированный метод Эйлера

11.3.5. Метод Рунге – Кутта

11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений

11.3.7. Общая характеристика одношаговых методов

3.8. Многошаговые методы

11.3.9. Методы прогноза и коррекции

11.3.10. Краткая характеристика методов прогноза и коррекции.

11.3.11. Выбор шага и погрешность решения.

11.3.12. Жесткие задачи

11.4. Имитационное моделирование систем

11.4.1. Принципы имитационного моделирования

11.4.2. Объекты моделирования

11.4.3. Динамическая модель исследуемого объекта

11.4.4. Построение имитационных моделей динамических систем

11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши

11.4.6. Синтез имитационной модели на основе структурной схемы

11.5. Теоретические основы построения математических моделей систем

11.5.1. Компонентные и топологические уравнения

11.5.2. Компонентные и топологические уравнения механической системы

11.5.3. Компонентные и топологические уравнения электрической системы

11.5.4. Компонентные и топологические уравнения гидравлической системы

11.5.5. Компонентные и топологические уравнения тепловой системы

11.6. Метод электроаналогий

11.6.1. Сущность метода электроаналогий.

11.6.2. Электромеханические аналогии

11.6.3. Построение имитационных моделей методом электроаналогий

11.6.4. Плоское прямолинейное движение звеньев

11.6.5. Электрогидравлические аналогии

11.6.6. Электротепловые аналогии

Литература

Решение. Вычисляем выборочную статистику

=

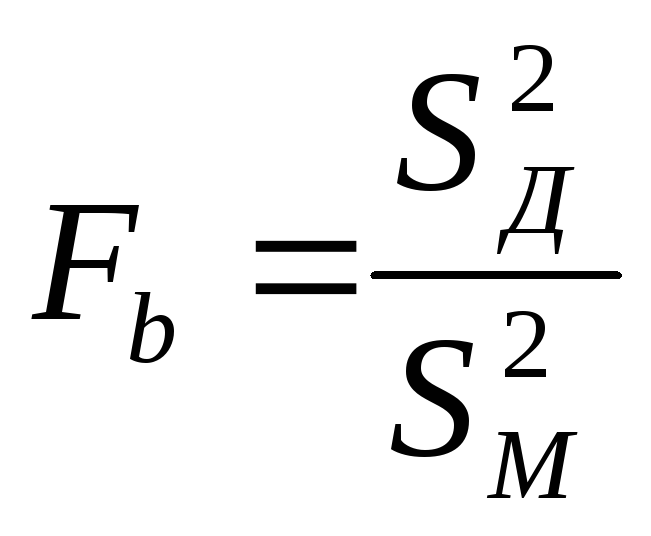По уровню значимости, а = 0,10 и числу степеней свободы k3 = nx — 1;

kM= ny — 1, т.е. k3 = 14; kM= 20 находим по таблице F1-a/2;14,20 = 2,23 (см. приложение 6). Сравниваем

Fb = 3,06 > F1-a/2;14,20 = 2,23.

Следовательно, гипотезу Н0 о равной точности автоматов отвергаем, так как разницу в дозировке химического вещества нельзя объяснить случайностью.

При больших объемах выборки статистику Fb можно определять по формуле:

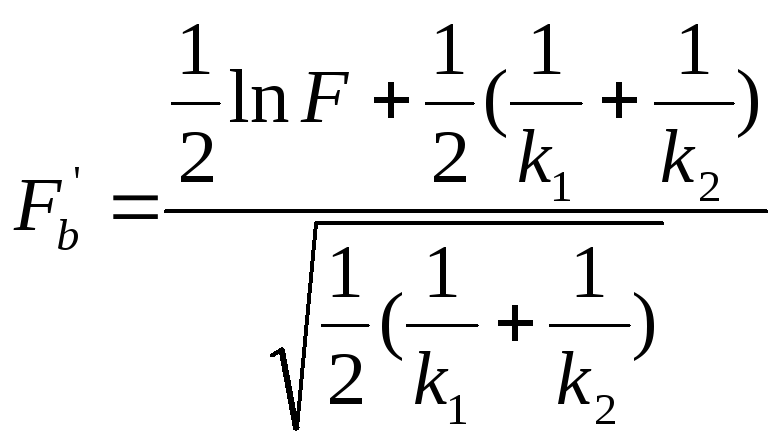
где .

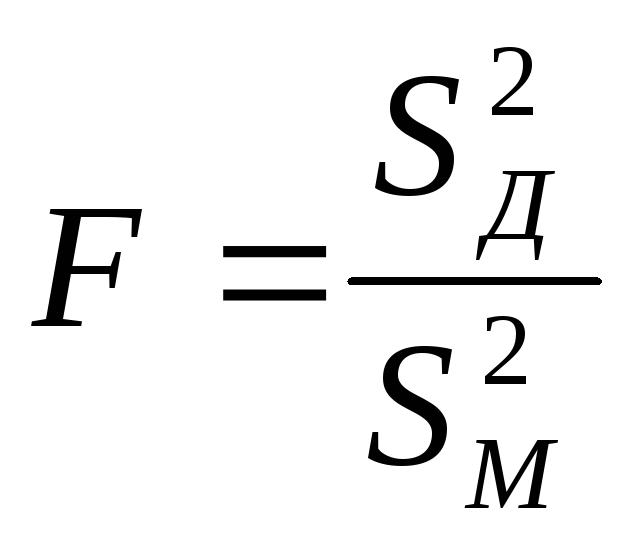При проверке гипотезы Но: D(x) = D(y) сравнивают F'b и U1-a/2, где — уровень значимости; U1-a/2 — квантиль уровня (1 — а/2) стандартного нормального распределения (см. приложение 1). При F'b < U1-a/2,

где Ф(U1-a/2) = 1 — а/2 и х = U1-a/2, гипотеза Н0 принимается, в противном случае, когда F'b ≤ U1-a/2, Н0 отвергается и принимается гипотеза Н1: D(x) ≠ D(y).

Если взята одна выборка n из генеральной совокупности, для которой предполагаемое значение дисперсии равно , хотя сама дисперсия D(x) неизвестна, то можно проверить при заданном уров- не значимости гипотезу Н0: D(x) = , при альтернативной гипоте- зе Н1: D(x) ≠ . Для проверки гипотезы Но определяют статистику

где S2 — выборочная дисперсия;

—гипотетическая дисперсия.

Гипотеза Н0 принимается, если удовлетворяется условие

;

в противном случае принимается альтернативная гипотеза Н1, где k — число степеней свободы, k = n — 1.

Критерий Пирсона и принимается по таблице (см. приложение 3).

Пример. Для проверки правильности высева семян взяты 20 участков. Отклонение от нормы высева оценивалось среднеквадратическим отклонением числа семян на участке, оно составило S =16 семян. Требуется при заданном уровне значимости а = 0,1 прове- рить нулевую гипотезу Но: D(x) =, при норме = 225. Конку- рирующая гипотеза Н1: D(x) ≠.

Р е ш е н и е. Определяем — статистику

При = 0,10 и k = 20 — 1 =19 определяем по таблице (см. приложение 3)

Записываем условие

,

т.е. принимается гипотеза Н1: D(x) = . Это означает, что сеялка настроена правильно в соответствии с заданной нормой и точностью высева.

Если исследуется нормально распределенные совокупности х1, х2, ..., хp, из которых извлечены независимые выборки n1, n2, ..., np различных объемов, для которых определены дисперсии , , ..., ,то при заданном уровне значимости можно проверить гипотезу Н0: D(x1) = D(x2) = ... = D(хp) по критерию Бартлетта. Для этого определяют статистику

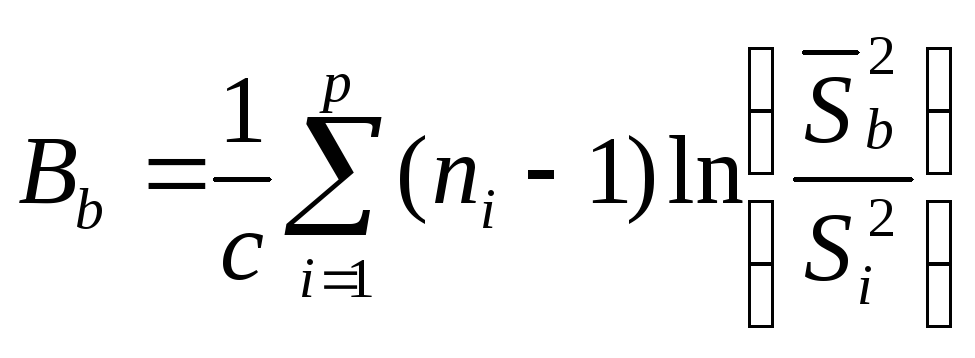
где

Величина является оценкой генеральной дисперсии D(x). Гипотеза Н0 принимается при условии

;

где k — число степеней свободы, k = р - 1; величина принимается по таблице (см. приложение 3). Критерий Бартлетта очень чувствителен к отклонениям от нормального распределения выборочных совокупностей. Если выборки равны n1, n2, ..., np, то для проверки гипотезы Н0: D(x1) = D(x2) = ... = D(xp) используют критерий Кохрена (Кочрена). Для проверки гипотезы Н0 вычисляют статистику

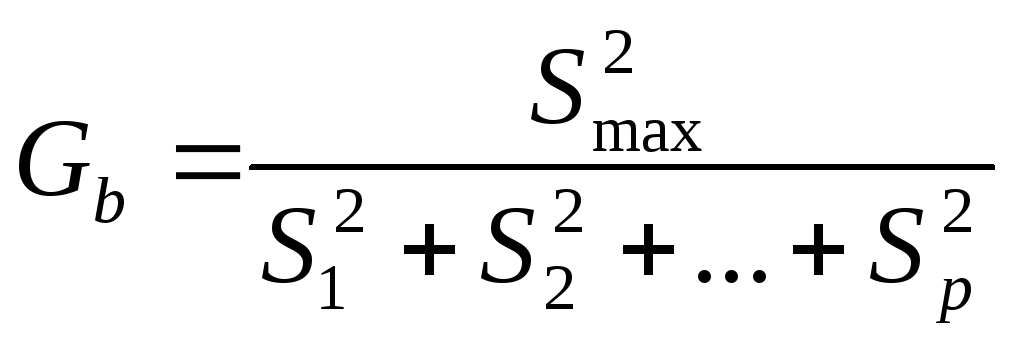
где — максимальная дисперсия из р дисперсий, т.е.

Полученное значение Gb сравнивают с критическим значением , k = n - 1; n — объем одной выборки. Гипотеза Н0 принимается при условии

в противном случае принимается гипотеза Н1: D(x1) ≠ D(x2) ≠ ... ≠ D(xp). Значение принимается по таблице (см. приложение 7). Пример. На 17 предприятиях региона в течение семи месяцев изучалась загрязненность промышленных стоков. Вычисленные эмпирические дисперсии для каждого из этих месяцев оказались равными: 0,067; 0,136; 0,168; 0,068; 0,066; 0,102; 0,107. Необходимо проверить гипотезу Н0 об отсутствии существенного различия в загрязненности промышленных стоков за семь месяцев. Решение. Вычисляем статистику

При уровне значимости = 0,05; р =7; k =17 — 1 =16; F1-0,05;7;16= 0,27 (см. приложение 7). Тогда

Gb = 0,235 < F1-0,05;7;16 = 0,27,

т.е. гипотеза H0 об отсутствии существенного различия в загрязненности промышленных стоков в течение семи месяцев принимается. Проверка статистических гипотез об однородности выборок. Для проверки однородности независимых выборок (х1, х2,..., хp) и (у1, у2, ..., уn2) случайных величин х и у выдвигаем нулевую гипотезу H0 о равенстве функций распределения H0: F(x) = F(y), при уровне значимости и конкурирующей гипотезе Н1: F(x) ≠ F(y). Если объем каждой из выборок не превосходит 25, проверку гипотезы H0 проводят с помощью статистики Wb. Для определения Wb статистики располагают варианты обеих выборок в возрастающем порядке (табл. 2.8). Например, для выборок nx: 3, 4, 6, 10, 13, 17 и ny: 1, 2, 5, 7, 16, 20, 22 общий ряд будет иметь вид

Таблица 2.8

Определение вариантов выборок

Порядковый номер

1

2

3

4

5

6

7

8

9

10

11

12

13

Значение

1

2

3

4

5

6

7

10

13

16

17

20

22

Варианты

y1

y2

х1

х2

y3

x3

y4

x4

x5

y5

x6

y6

y7

Определяем сумму порядковых номеров варианта выборки nx:

3+4+6+ 8+9+ 11=41.

Эта сумма принимается в качестве статистики Wb(x) = 41. Для проверки гипотезы Hо используется условие:

Wн.к < Wb(x) < Wв.к

где Wн.к и Wв.к — нижнее (н.к) и верхнее (в.к) критические значения критерия Вилкоксона (Уилкоксона). При заданном значении уровня значимости и объемах выборок nx и ny величина Wн.к. определяется по таблице (см. приложение 8). Для нашего примера при = 0,01, nx = 6, ny = 7, величина

Смотрите также файлы