ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1172
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
Wн.к
=
Если объем хотя бы одной из выборок превышает величину 25, значение Wн.к определяется по формуле
где zкр определяется из условия по таблице (см. приложение 1).
x
= zкр
Верхнее критическое значение величины Wв.к во всех случаях определяется по формуле
Wв.к = (nx + ny +1)nx - Wн.к.
Для нашего примера
Wв.к = (6 +7 +1)6 — 24 = 60.
Тогда условие принятия гипотезы Н0: F(x) = F(y) и
Wн.к = 24 < Wb(x) < Wв.к = 60
соблюдается.
Следовательно,
можно
считать,
что
выборки
nx
и
ny
принадлежат
одной
генеральной
совокупности,
т.е.
выборки
однородны.
Проверка
статистических
гипотез
о
виде
распределения
случайных
величин.
При
построении
математической
модели
исследуемых
процессов
часто
возникают
задачи
сопоставления
полученного
материала
экспериментов
с
известными
теоретическими
распределениями.
Если
сопоставить
вероятность
попадания
в
интервалы,
на которые
разбита
выборка,
с
соответствующими
частотам
и,
полученными
из
наблюдений,
или
проводить
графическое
сравнение
полигонов
и
гистограмм
с
некоторой
теоретической
функцией
распределения,
то
можно
получить
представление
о
степени
близости
теоретического
и
эмпирического
распределений.
Наиболее
широко
для
проверки
статистических
гипотез
о
сходимости
теоретического
и
эмпирического
распределения
используется
критерий
Пирсона
(
—
хи-квадрат).
Рассмотрим
его
применение.
Пусть
вся
область
изменения
случайной
величины
х
разбита
на конечное
число
k(i
=
1,
2,
...,
k)
интервалов
(в
случае
непрерывной
величины)
или
групп
(для
дискретных
величин).
Например,
в
статистический
ряд,
полученный
в
результате
эксперимента
(табл.
2.9).
Таблица 2.9
Статистический ряд, полученный в результате эксперимента
|
Значение величины хi |
x1 |
x2 |
… |
xi |
… |
xk |
|
Частота mi |
m1 |
m2 |
… |
mi |
…. |
mk |
Пусть Рi есть вероятность для х при заданном распределении F(x) принять значение, принадлежащее i-тому интервалу. Тогда те- оретическое значение частоты в этом интервале будет определяться, как mi,T = рin, где п — объем выборки.
Очевидно, что должны выполняться условия
;
.
Если проверяемая гипотеза H0: F(x) = F0(x) где F0(x) — предпо- лагаемое теоретическое распределение, из которого извлечена вы- борка, верна, то опытные значения тi и теоретические тi,T не должны значительно отличаться друг от друга, т.е. их расхождение не должно быть большим.
В
качестве
меры
расхождения
рассматривается
статистика
,
равная
При
проверке
гипотезы
Н0
статистика
сравнивается
при
заданном уровне
значимости
с
табличным
значением
При
условии
<
,
где
(k
-
1)
—
число
степеней
свободы,
гипотеза
Н0
принимается.
В
случае,
если
≥
,
гипотеза
Н0
отвергается
и
принимается альтернативная
гипотеза
Н1:
F(x)
≠ F0(x).
При проверке гипотез о виде распределения с помощью критерия Пирсона следует учитывать некоторые условия и допущения, влияющие на полученный результат.
1) Если гипотеза Н0 подтверждается, то это означает лишь су- ществование некоторой функции F1(х), которая приводит к тем же значениям рi что и проверяемая функция F0(x).
2) Рекомендуется число интервалов брать не менее 8 с количеством вариантов в интервале не менее 8, кроме крайних интервалов, в которых число вариантов может быть меньше 8.
Пример. Используя критерий Пирсона при уровне значимости α = 0,05 проверить, согласуется ли гипотеза Н0 о нормальном рас- пределении генеральной совокупности х с эмпирическим распреде лением выборки объема n = 200 (табл. 2.10).
Таблица 2.10
Выборка из генеральной совокупности
|
xi |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
2,1 |
|
mi |
15 |
26 |
25 |
30 |
26 |
21 |
24 |
20 |
13 |
Решение.
По
выборке
определяем
и
S2.
.
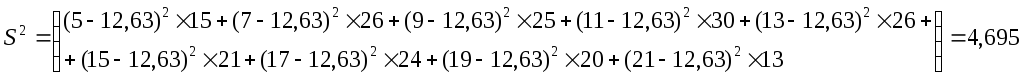
Составляем статистическую таблицу (табл. 2.11). Для столбца четыре вычисляем статистику
иi
=
(xi
-
)/S.
Например,
иi
=
=
-1,62 и
т.д.
По статистике иi находим рi по таблицам для нормального распределения (см. приложение 9).
pi = φ(ui).
Например,
pi = φ(u1) = φ(-1,62) = 0,1074 и т.д.
Теоретическую частоту вычисляем с учетом ширины интервала результатов наблюдения n = хi+1 - хi = 2 по формуле
тi,T
=
nh
φ(иi)/S.
Например, для х1
mi,T
=
=
9,15
и
т.д.
Таблица 2.11
Статистическая таблица
|
Номер |
Частота mi |
Статистика ui |
Вероятность pi |
Теорети- ческая частота mi,т |
Относительная разность частот |
|
|
интервала |
варианта xi |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
5 |
15 |
— 1,62 |
0,1074 |
9,15 |
3,74 |
|
3 |
7 |
26 |
— 1,20 |
0,1942 |
16,55 |
5,39 |
|
4 |
9 |
25 |
— 0,77 |
0,2966 |
25,27 |
0,01 |
|
5 |
11 |
30 |
— 0,35 |
0,3752 |
32,00 |
0,13 |
|
6 |
13 |
26 |
0,08 |
0,3977 |
33,90 |
0,23 |
|
7 |
15 |
21 |
0,51 |
0,3503 |
29,85 |
2,62 |
|
8 |
17 |
24 |
0,93 |
0,2589 |
22,05 |
0,17 |
|
9 |
19 |
20 |
1,36 |
0,1582 |
13,50 |
3,13 |
|
10 |
21 |
13 |
1,78 |
0,0818 |
7,0 |
5,14 |
|
|
200 |
- |
- |
189,27 |
20,56 |
|