Файл: Математическое моделирование в экологии.doc

2) при ограниченном потреблении жертв хищниками

3) для определения времени, необходимого для эволюционных явлений при росте популяций величина у рассматривается как функция от времени t, тогда

если между яйцекладкой и формированием взрослой особи проходит время τ, то

При оценке эпидемий с инкубационным временем τ модель может иметь следующий вид. Пусть Y_m есть общая популяция, а Y — зараженная популяция, так что (Y_m - Y) — подверженная заболеванию популяция. Учитывая запаздывание, вызванное наличием инкубационного периода, текущая вероятность заражения зависит от размера инфицированной популяции в момент (t - τ), что можно записать в виде:

(11.13)(5.13)

где μ — вероятность заражения организма в единицу времени;

с — темп естественного выздоровления. Уравнение (5.13) можно записать в виде

Функциональные модели наиболее распространены при описании процессов преобразования одного параметра в другой, при анализе расходов (доходов), структурном анализе и во многих других случаях.

Моделирование процессов выживаемости популяций. Математическое моделирование является одним из наиболее распространен- ных методов изучения окружающей природной среды, который по- зволяет при минимальных затратах получить достоверную инфор- мацию об изучаемых объектах.

При помощи моделирования реальные процессы, происходящие в окружающем мире, можно описывать в виде формальных характеристик. Математическое моделирование позволяет классифицировать и систематизировать фактические материалы, прогнозировать развитие ситуации. Часто математическое моделирование является единственным способом решения определенных типов задач. Рассмотрим динамику выживания определенного поколения особей какой-либо популяции от рождения до полного исчезновения. Формализуем условия задачи.

Итак, в начальный момент времени t = 0 (например, в момент метания рыбами икры или откладывания яиц птицами) количество особей в наблюдаемом поколении было N₀. Пусть в момент времени z их количество стало N, а через некоторое время (t + Δt) — (N — ΔN). За время Δt наблюдаемая группа уменьшилась на ΔN особей. Тогда скорость уменьшения особей в наблюдаемой группе будет равна:

Предположим, что скорость уменьшения количества особей в рассматриваемом поколении прямо пропорциональна их количеству в данный момент времени. Тогда

где k — коэффициент пропорциональности, характерный для популяции. Решаем уравнение:

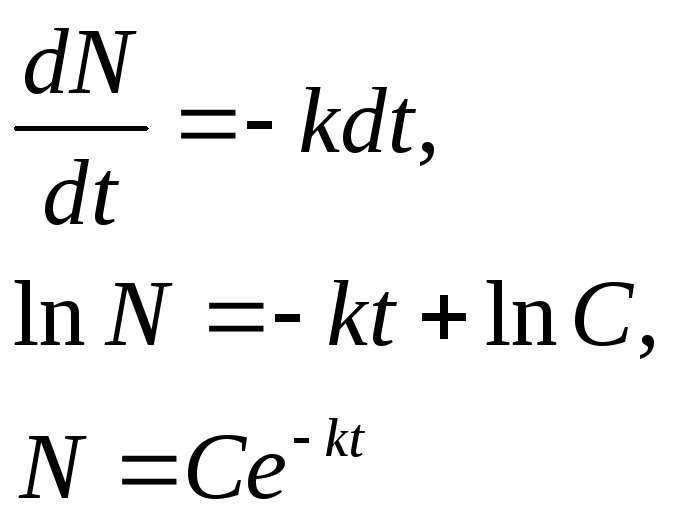
Так как в начальный момент времени t₀= 0 (при рождении) количество особей в популяции было N₀, то

В итоге получаем:

N=N₀е^-kt

Эта формула представляет собой простейшую математическую модель выживания особей в какой-либо популяции и основывается на сделанном ранее допущении, что скорость уменьшения количества особей в рассматриваемой одновозрастной группе прямо пропорциональна ее общему количеству в каждый данный момент времени.

Каждой популяции свойственна своя математическая модель выживаемости, которую можно представить графически в виде ниспадающей кривой. Типичные примеры таких кривых представлены на рис. 11.4.

Кривая А представляет собой идеальную кривую выживаемос- ти для популяции, где главным фактором смертности является старение. Такая кривая наиболее характерна для человеческого рода.

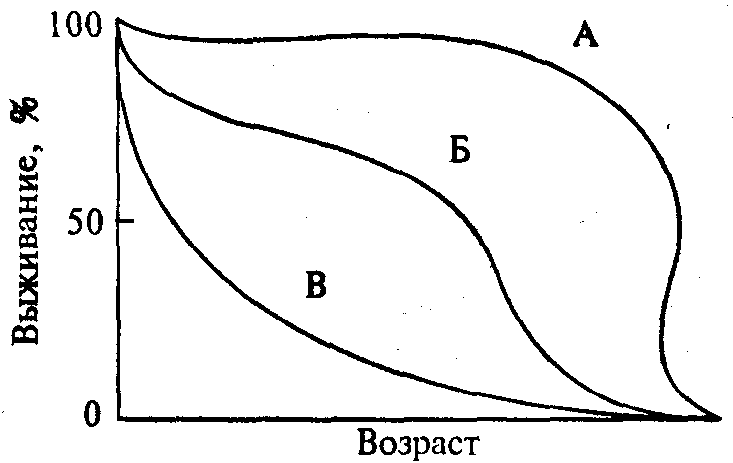
Рис. 11.4. Типы кривых выживаемости

Процесс выживаемости в популяции с высокой смертностью в ранний период описывает кривая Б. Эта самая распространенная модель выживаемости в растительном и животном мире. И, наконец, кривая В описывает процесс выживаемости популяции, когда в основном внешние факторы определяют смертность. Гибель особей начинается задолго до процесса старения.

Рассмотрим другую задачу, связанную с ростом численности особей в популяции. Формализуем ее.

Пусть в некоторый момент времени t₀ количество особей в некой популяции будет N₀, а по прошествии некоторого времени Δt количество особей увеличилось до N. Отношение

будет характеризовать среднюю скорость прироста популяции. При Δt→∞ этот показатель стремится к некой норме r, присущей естественному приросту для рассматриваемого вида

Решая это уравнение, получим:

N= N₀ еⁿ.

В действительности такое неограниченное экспоненциальное возрастание численности особей присуще лишь человеческому роду. Для остальных же живых организмов существует ряд лимитирующих факторов, не позволяющих бесконечно возрастать их численности. Причем часто эти факторы влияют на численность не столь прямо, сколько опосредованно, через изменение системы биотических взаимодействий. Из этого можно сделать вывод, что суще- ствует предел, представляющий собой максимальную численность популяции К, к которому будет бесконечно стремиться кривая рос- та популяции. В таких условиях численность популяции N изменяется в соответствии с выражением

(11.14)(5.14)

где α = r/К.

Площадь, заключенная между кривой, описываемой этим выражением, и кривой, описываемой выражением (11.14)(5.14), показывает сопротивление среды росту популяции (рис. 11.5).

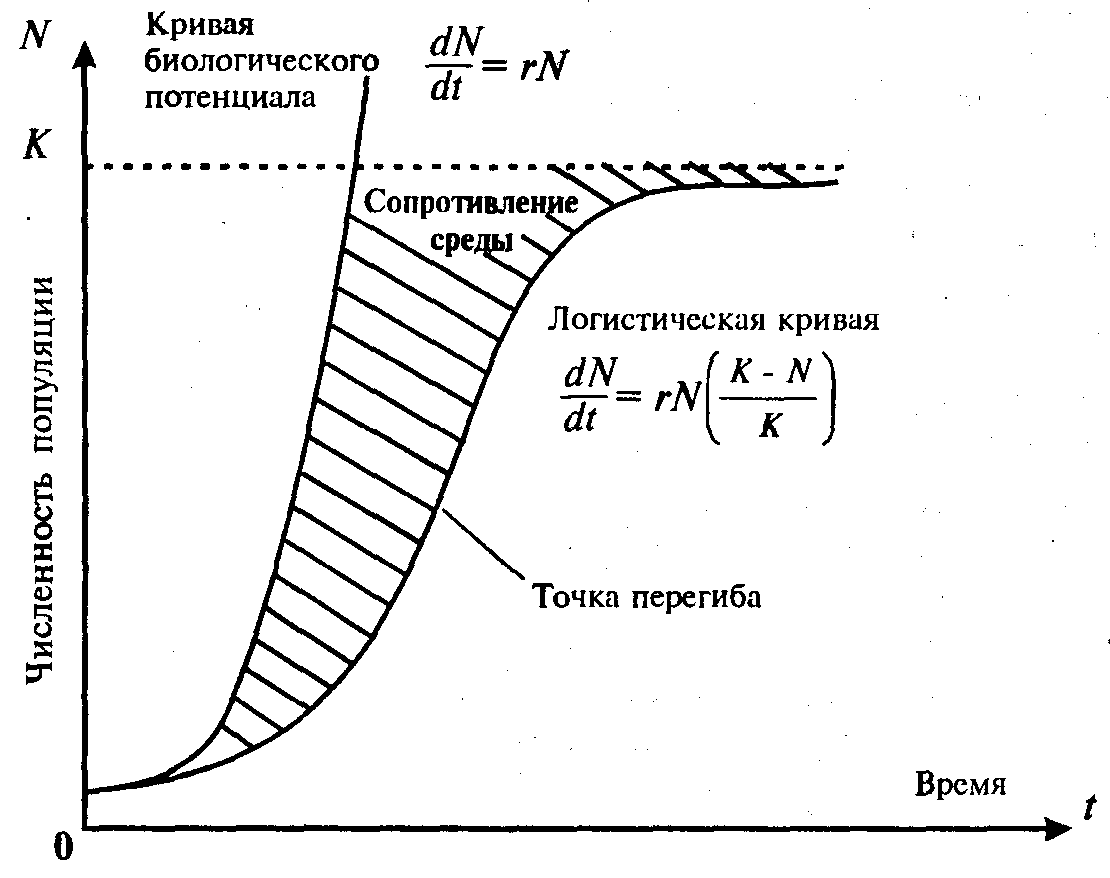
Рис. 11.5. Рост численности популяции

Чем многочисленнее популяция, тем сильнее сопротивление среды. Коэффициент сопротивления среды описывается с помощью выражения

Производная от выражения (5.14) является скоростью роста численности популяции

Несмотря на то, что выражение (5.14) достаточно хорошо аппроксимирует эмпирические данные, его предпосылки не могут считаться достаточно полными. Реальная картина гораздо сложнее. В природе число особей каждого вида никогда не остается постоянным, а колеблется около некоторого среднего значения. Этим проявляется конкуренция внутренних и внешних факторов, регулирующих численность популяции. Внешние факторы влияют главным образом на показатель смертности т, а внутренние b— рождаемости. Разность этих показателей

r = b — m

определяет демографические возможности популяции. Для оценки демографической структуры популяции необходимо собрать сведения о смертности и рассчитать ожидаемую продолжительность жизни в различных возрастных классах, составляющих популяцию.

назад

Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.

Многие экологические процессы развиваются во времени и представляют собой динамические процессы, которые характеризуются изменением скорости течения. Такие процессы могут рассматриваться с точки зрения оценивания состояния системы в заданные моменты времени.

Определение состояния процесса означает оценивание зависимых переменных этого процесса. Можно различить три типа оценивания состояния. Если проведены наблюдения в интервале от t₀ до t_i, то оценивание вектора состояния в момент времени t классифицируется как:

1) интерполяция (сглаживание), если t < t_i; 2) фильтрация, если t = t_i; 3) экстраполяция (предсказание), если t> t_i.

Если модель процесса представляет собой дифференциальное уравнение, то эксперименты следует проводить по планам, которые должны давать независимые ошибки при измерениях, а модель, коэффициенты которой требуется оценить, должна быть адекватной.

Модель должна содержать: дифференциальные уравнения и граничные и(или) начальные условия. Последние необходимы для того, чтобы модель имела единственное решение.

В модели с начальными значениями, содержащей одно дифференциальное уравнение, число задаваемых начальных условий должно равняться порядку наивысшей производной. Для системы дифференциальных уравнений первого порядка обычно задается по одному начальному условию на зависимую переменную в каждом уравнении.

В модели с граничными значениями соответствующее число значений зависимой переменной или ее производных задается при различных значениях независимых переменной, т.е. не только в начале, но и в конце интервала изменения независимой переменной. Если общее решение модели известно, заданные значения можно подставить в общее решение и вычислить произвольные постоянные.

Простейшей моделью является обыкновенное дифференциальное уравнение первого порядка с постоянным коэффициентом

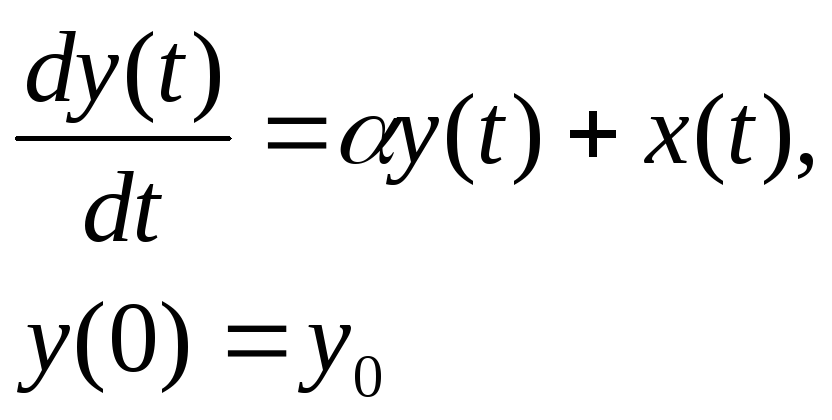
которое имеет решение

,