ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1139
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
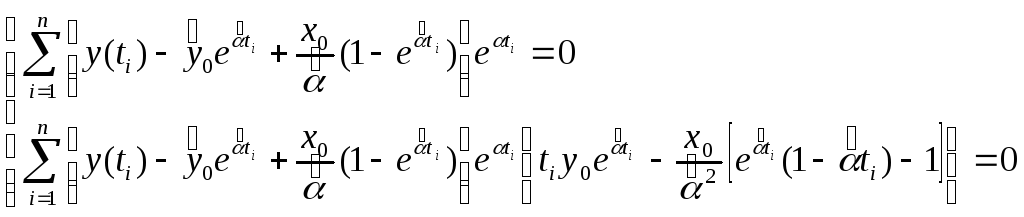
Используя функцию Ф следует учитывать:
1) ненаблюдаемая ошибка добавляется к детерминированному отклику специальным образом;
2) в оценках используются одновременно все n откликов;
3) в критерии не входит никакая априорная статистическая информация, за исключением, быть может, той, которая вводится с помощью матрицы Г.
назад
Лекция 13. Статистические модели динамики.
Многие процессы в экологии могут быть представлены в виде статистических моделей. Существует много различных причин тому, что факторы в этих процессах принимают случайное значение. Иногда случайность предопределена самой физической сущностью явлений, в других случаях сказывается неполнота информации о данной величине фактора или инструментарий не позволяет исследователю получить всю необходимую информацию. Наконец, неопределенность может возникнуть потому, что модель действительного процесса выбрана с большими допущениями или ошибками.

Рис. 13.7. Схема статистической модели
Если X(t) — случайная переменная на входе системы, а Y(t)— случайная переменная на выходе системы, обусловленная перемен- ной X(t), то модель процесса можно описать обыкновенным дифференциальным уравнением порядка n
![]()
![]() (13.15)(5.15)
(13.15)(5.15)
где
Y(n)(t)
=
![]() ?производная
степени
n
от
Y(t);
?производная
степени
n
от
Y(t);
αi — постоянные, не являющиеся случайными величинами. В начальных условиях также присутствует элемент случайности
Y(n-1)(0) = Y(m-2)(0) = ..... = Y(0) = 0 . (13.16)(5.16)
Предположим, что требуется по известным данным на входе и выходе системы найти значение Y(t) и ее автокорреляционную функцию, поскольку плотность распределения вероятности неизвестна. Вычисляя математическое ожидание от обеих частей уравнения (13.15)(5.15) и равенства (13.16)(5.16), и используя формулу для вычисления математического ожидания величины X(t)
![]() (123.17)(5.17)
(123.17)(5.17)
получаем
![]() Д
(13.18)(5.18)
Д
(13.18)(5.18)
![]() (13.19)(5.19)
(13.19)(5.19)
![]()
![]() ,
,
где α — некоторая постоянная.
Уравнения (5.18) и (5.19) являются детерминированной моде- лью для μy и дают искомое решение для μy
![]() ,
(13.20)(5.20)
,
(13.20)(5.20)
где μp(t) — частное решение неоднородного уравнения (13.18)(5.18), а остальные члены правой части равенства (13.20)(5.20) представляют собой общее решение соответствующего однородного уравнения.
Следовательно, если заданы математическое ожидание X(t) и значения коэффициентов в уравнении (13.18)(5.18), можно найти детерминированное решение моделей, представленных на рис. 5.7.
Используя определение автокорреляционной функции
Rxx(t1, t2) = e{X(t1)X(t2)},
можно показать, что
![]()
![]()
Следовательно,
![]() (13.21)(5.21)
(13.21)(5.21)
Автокорреляционную функцию RYY(t1,t2) для Y(t) можно получить следующим образом. Сначала умножаем уравнения (13.15)(5.15) и (13.16) (5.16) для t = t2 на x(t1)
![]() ;
;
![]() (13.22)(5.22)
(13.22)(5.22)
и вычисляем почленно, используя свойство (5.17), математическое ожидание от обеих частей этих равенств. В результате получим:
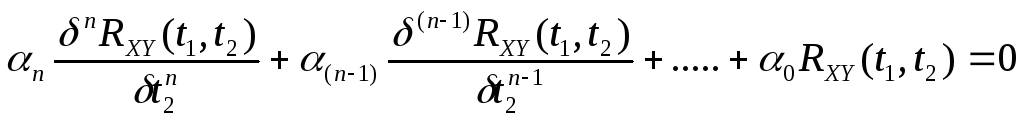 ;
(13.23)(5.23)
;
(13.23)(5.23)
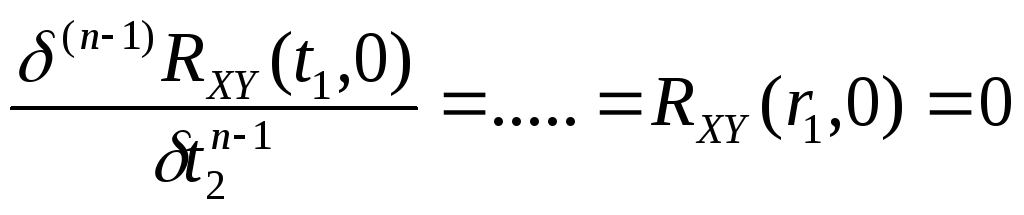 .
(13.24)(5.24
)
.
(13.24)(5.24
)
Уравнение (13.17)(5.17) представляет собой обыкновенное дифференциальное урав-нение для RXY(t1,t2) с независимой переменной t2 параметром t1.
Таким образом, при условии, что автокорреляционная функция RXX(t1,t2) RRrrКкк задана, уравнения (13.23)(5.23) и (13.24)(5.24) можно использовать для вычисления взаимной корреляционной функции RXY(t1,t2) RRrrКкк. Затем умножим уравнения (5.15) и (5.16) для t =t1, на Y(t2)
Y(t2)[ αnY(n)(t1)+.....+ α0Y(t1)] Y(t2)X(t1), (13.25)(5.25)
Y(t2)Y(0)=….=Y(t2)Y(0)=0 (13.26)(5.26)
и снова вычисляя математическое ожидание от обеих частей, получим обыкновенное дифференциальное уравнение RYY(t1,t2).
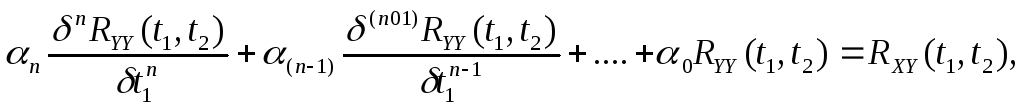 (13.27)(5.27)
(13.27)(5.27)
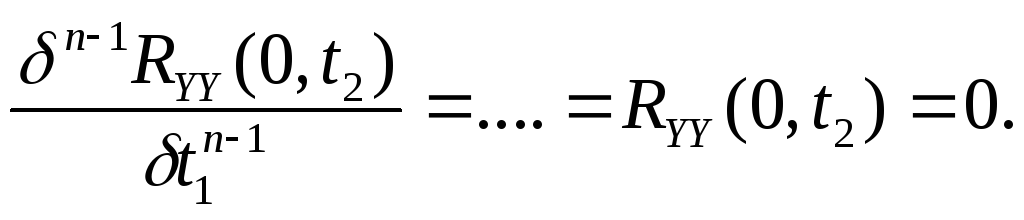 (13.28)
(5.28)
(13.28)
(5.28)
Для того чтобы найти RYY(t1,t2), нужно решить уравнения (13.23)(5.23) и (13.24)(5.24) для RXY(t1,t2), предполагая, что функция RXY(t1,t2) известна. Затем подставить результат в правую часть уравнения (13.27)(5.27), которое после этого можно разрешить относительно искомой функции RYY(t1,t2) с учетом условия (13.28)(5.28).
Пример. Имеется резервуар, в котором загрязненная вода перемешивается с чистой и сбрасывается в реку. Объем резервуара V, скорость подачи воды F, концентрация загрязняющих веществ на входе в резервуар С0 — случайная величина. На выходе концентра- ция С — также случайная величина.
Вычислить среднее значение концентрации, дисперсию и ав- токорреляционные функции, если концентрация раствора пред- ставляет собой броуновскую случайную величину.
Р е ш е н и е. Концептуальная модель системы представлена на рис. 13.8.
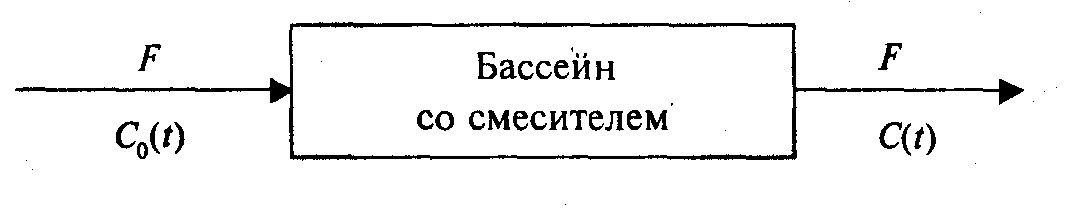
Рис. 13.8. Схема смесителя
Броуновское движение на молекулярном уровне оказывается весьма сложным, но при макроскопическом рассмотрении важно определить лишь математическое ожидание перемещения, отождествляемого со случайной величиной X(t). Если для одномерного движения начальное положение частицы принять равным нулю X(0)=0, то одномерная плотность распределения вероятности определится выражением
![]()
где α — некоторая постоянная.
Типичный участок пути частицы показан на рис. 13.9. Математическое ожидание будет определяться по формуле (13.17)(5.17) при
![]()
![]()
![]()
где α — параметр плотности распределения вероятности дл С0 .
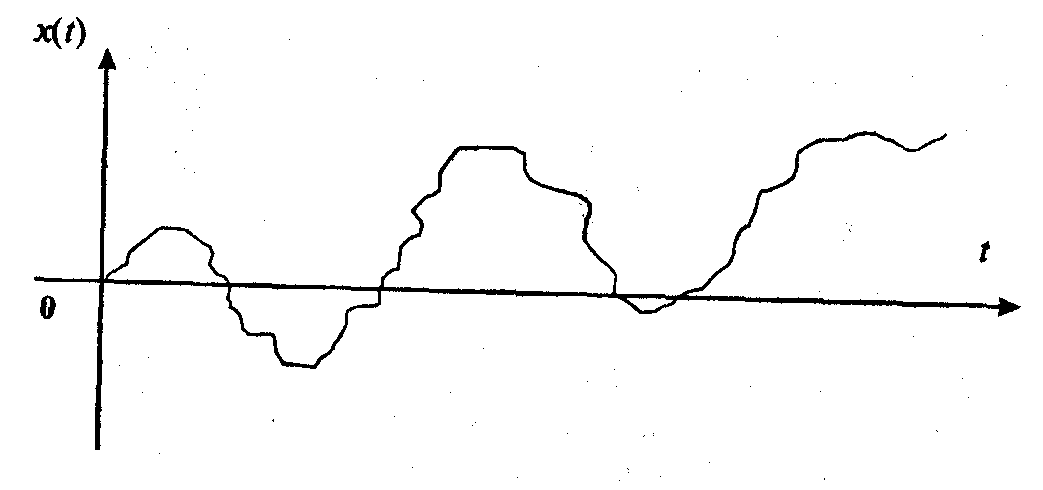
Рис. 13.9. Типичный участок пути частицы
Уравнения (13.22)(5.22) и (13.23)(5.23) для этой модели принимают вид ,
![]()
![]()
![]()
и имеют следующее решение
![]()
где t* = V/F
Уравнения (5.27) и (5.28)
![]()
![]()
имеют решение
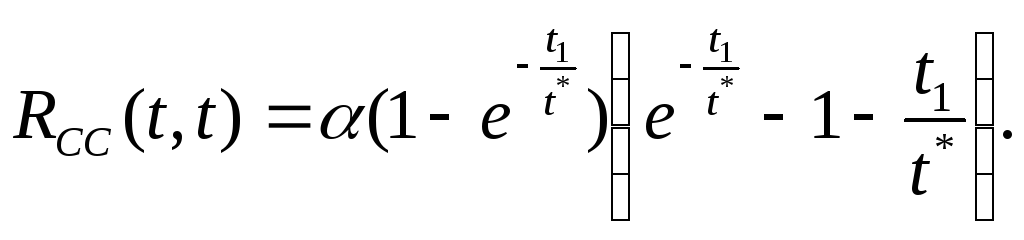
Таким образом, автокорреляционную функцию случайной функции на выходе резервуара можно вычислить даже в том случае, если плотность распределения вероятности для этой функции неизвестна.
Более общей моделью является модель, содержащая систему линейных (по зависимым переменным) обыкновенных дифференциальных уравнений первого порядка с постоянными коэффициентами, например рис. 13.10.
![]()
![]()
![]()