Файл: Математическое моделирование в экологии.doc

3.2.2. Выборочный метод в экологометрике.

Наблюдения, проводимые над экологическими объектами, могут охватывать всю совокупность или группу объектов. В первом случае наблюдение будет называться сплошным, а во втором — выборочным.

Задача выборочного метода состоит в том, чтобы на основе знаний свойств выборки можно было сделать какие-либо утверждения о свойствах всей совокупности объектов, которую называют генеральной совокупностью.

Под генеральной совокупностью для данного объекта исследования понимается бесчисленное множество таких же объектов, которые можно считать похожими по тем или иным свойствам или характеристикам. Однако между этими похожими объектами можно также обнаружить некоторые свойства и характеристики, отличающие один объект от другого. Например, изучая воздушную среду отдельного города, в качестве генеральной совокупности можно взять всю воздушную среду планеты. В то же время при изучении содержания кислорода в воздухе мы должны учитывать высоту местности над уровнем моря и поэтому различные города можно отнести к различным группам по этому признаку.

Таким образом, совокупность объектов, которые объединены в нечто однородное по некоторым признакам и в то же время по другим признакам расчленены на группы, включающие в себя определенное число объектов, называется статистической совокупностью. При этом те признаки, по которым совокупность расчленяется на группы, называются группированными признаками, которые в свою очередь подразделяются на качественные (атрибутивные) и количественные (вариационные) признаки.

Статистические совокупности могут быть расчленены одновременно по нескольким признакам. В связи с этим различают одномерные, двумерные и многомерные статистические совокупности. Они могут также состоять из дискретных объектов и непрерывных множеств. Признаки объектов или множеств могут также принимать либо дискретные, либо непрерывные значения. Если генеральная совокупность объектов определена, то выбранные из нее случайным образом и объекты называют случайной выборкой. Математическая статистика имеет дело только со случайными выборками. Числовые или нечисловые характеристики изучаемых объектов, полученных в результате наблюдений или измерений у каждой единицы выборки, называют статистическими данными.

Различают следующие виды отбора объектов из генеральной совокупности в выборку:

1) типический, или групповой, когда генеральная совокупность предварительно делится на типические группы (например, участки, делянки, районы);

2) серийный, или гнездовой, когда генеральная совокупность делится на серии, или гнезда;

3) механический, когда генеральную совокупность предварительно разбивают на несколько частей (или групп) и затем из каждой части отбирают в выборку по несколько объектов, представителей этих частей. Если учесть, что изучение выборки преследует цель исследования свойств и характеристик генеральной совокупности, то выборка должна быть представительной (репрезентативной). Это означает, что ее объем должен быть не менее некоторого специального определенного объема, что будет рассмотрено далее.

Исследования или измерения каких-либо свойств или характеристик отдельных объектов выборки представляются в виде статистического ряда, они могут быть дистрибутивные, вариационные, динамики, или временные.

Дистрибутивные ряды служат для разделения объектов выборки по каким-либо признакам, заранее известным, например, людей по группам крови.

Вариационные ряды показывают закономерность распределения единиц изучаемой выборки по ранжированным значениям варьирующего признака, например, пробы воздуха по содержанию пылевых частиц.

Ряды динамики (временные) показывают закономерность изменения варьирующего признака в зависимости от времени.

При статистической обработке не следует упускать из внимания экологический смысл изучаемого объекта, который всегда устанавливает границы исследования. Таким образом, выборка — группа объектов, отличающихся некоторыми особенностями:

• это часть генеральной совокупности;

• объекты в выборку отбираются в случайном порядке определенным способом;

• объекты выборки исследуются для определения характеристик самой выборки и для оценки характеристик генеральной совокупности.

Основное правило — соблюдение равной вероятности попадания в выборку любого объекта генеральной совокупности, т.е. вы- бор должен быть совершенно случаен.

Построение статистического ряда. Пусть имеется некоторое множество N объектов, которое рассматриваем как генеральную совокупность, характеристику (признак) Х которой нам необходимо изучить. Так как N слишком велико, то для определения характеристики берем из N некоторое подмножество объектов n, которое назовем выборкой.

Если выбор каждого из n объектов производится независимо один от другого по всему множеству N случайным образом, то та- кую выборку можно назвать случайной или статистической. Ре- зультатом выборки n является совокупность х₁, х₂, ..., х_n зафиксиро- ванных значений характеристики (признака) Х.

Характеристика Х является случайной величиной. Если опыты (наблюдения) производились в одинаковых условиях и независимо друг от друга, то-выборку (х₁, х₂, ..., х_n) можно рассматривать как - n-мерный случайный вектор, где величины х_i независимы, и каждая из них распределена так же, как и случайная величина Х в генеральной совокупности. В этом случае можно сказать, что выборка (х₁, х₂, ..., х_n) взята из генеральной совокупности случайной величины Х с теорети- ческой функцией распределения F(x).

Результаты опыта, записанные в порядке возрастания х, называют вариационным рядом (расположение х в порядке возрастания называют ранжированием ряда), величину х, называют вариантой. Например, при исследовании пораженности лесного массива выявлено на одном гектаре пораженных деревьев:

4; 12; 11; 13; 15; 7; 15; 6; 4; 9; 10; 15.

Результаты опыта представлены в виде вариационного ряда:

4; 4; 6; 7; 9; 10; 11; 12; 13; 15; 15; 15.

В случае, когда в n опытах величина х,. встречается m_i раз, то число m называют частотой величины х_i (в нашем примере для х_i = 15, m_i = 3), а отношение частоты к общему числу опытов n называют относительной частотой (или частостью, вероятностью)

W_i = m_i/n

Для данного примера для W_i = 3/12 = 1/4, при х_i = 15. Очевидно, что сумма частот равна:

= n, а частостей =1,0

где k — число различных групп значений величин х.

Результаты наблюдений можно записать в виде последовательности пар чисел (х_i, m_i). Такую запись называют статическим рядом (табл. 3.1).

Статический ряд последовательности пар чисел

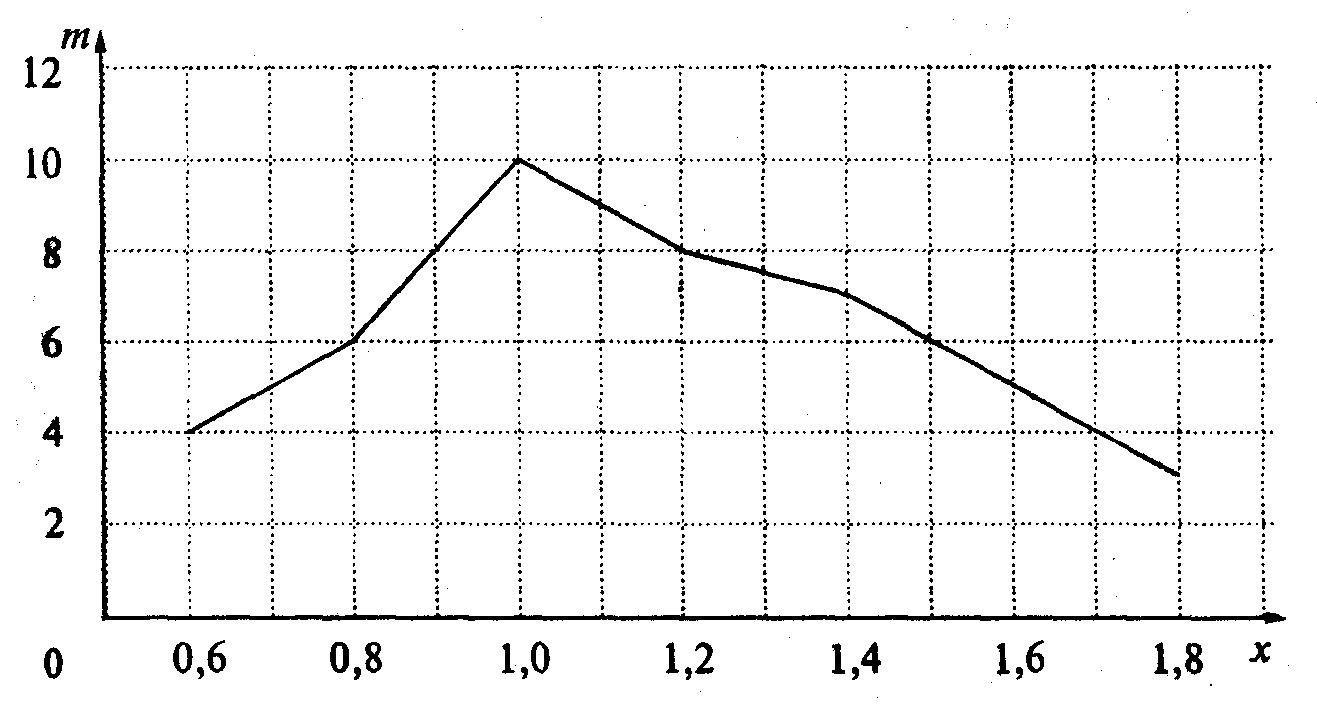Можно построить в системе координат (х, m) график с точками (х₁, m₁), (х₂, m₂), ..., (х_k, m_k) и соединить полученные точки ломаной линией, которую называют полигоном частот выборки или полиго- ном

Рис. 3.1. Полигон распределения х.

распределения (см. рис 3.1).

Полигон строится для таких величин, которые принимают дискретные значения х. Для непрерывных величин строится гистограмма распределения (рис. 2.2), построение которой рассмотрим на примере.

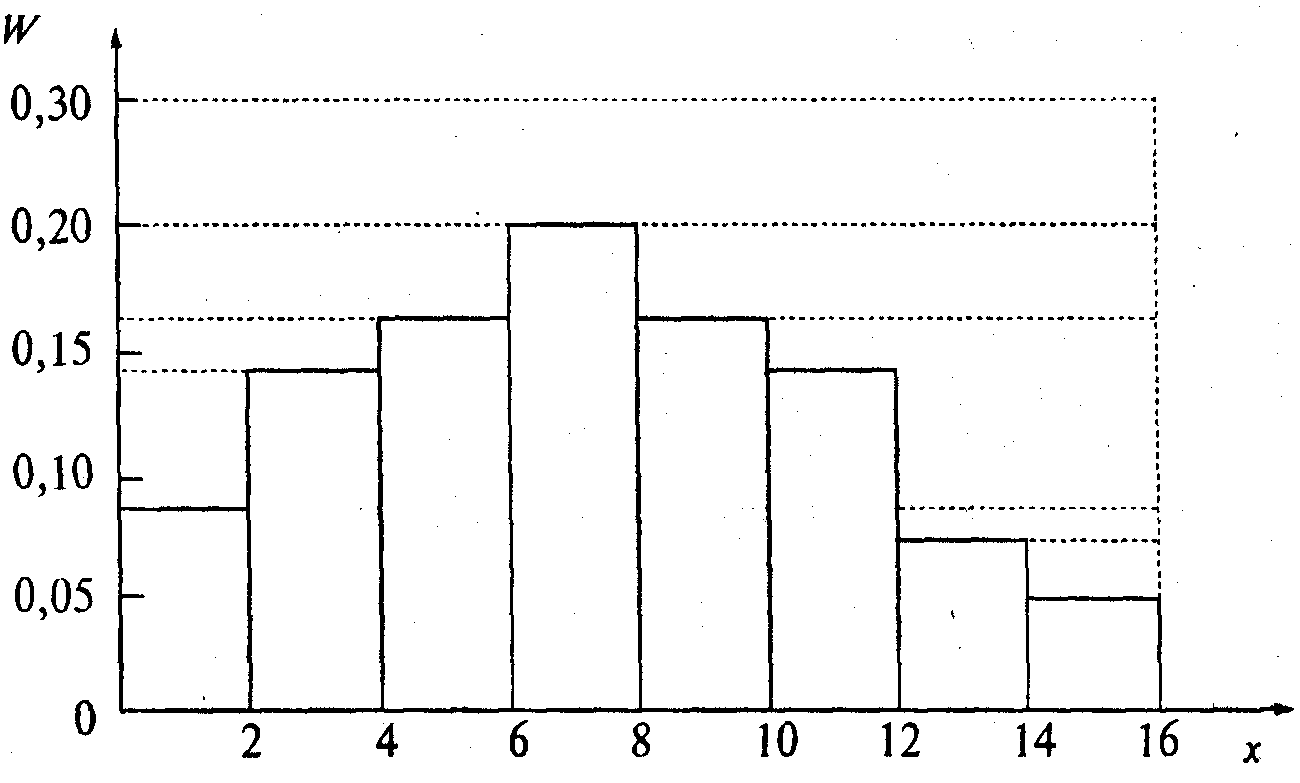
Рис.3.2. Гистограмма распределения нитратов в огурцах

Пример. Вариационный ряд, записанный по результатам 64 опытов по определению содержания нитратов (мг/кг) в огурцах, поставляемых в магазин из совхоза, имеет вид:

0,1;0,2;0,2;1,0;1,0;1,5;2,1;2,1;2,2;2,3;2,5;3,5;3,8;3,9;4,2; 4,2; 4,4; 4,5;

5; 5,0; 5,5; 5,6; 5,8; 6,0; 6,2; 6,3; 6,5, 6,8; 6,8; 6,8; 7,0; 7,5; 7,8; 7,8; 7,8; 7,8; 8;

8; 8,6; 8,8; 9,0; 9,5; 9,5; 9,5; 9,5; 9,5; 10,0; 10,0; 10,0; 11,3; 11,8; 11,8;

11,8; 11,9; 12,0; 12,0; 12,8; 13,2; 13,8; 13,8; 14,0; 14,5; 15,0; 15,9.

Здесь наименьшее значение Х_min = 0,1; наибольшее — Х_max = 15,9. Разницу между наибольшим и наименьшим значением х называют размахом (R), который равен

R = Х_max - Х_min = 15,9 — 0,1 = 15,8.

Выбираем число интервалов для группировки данных. Число интервалов можно ориентировочно выбирать по табл. 2.2 в зависимости от объема выборки n.

Таблица 3.2