Файл: Математическое моделирование в экологии.doc

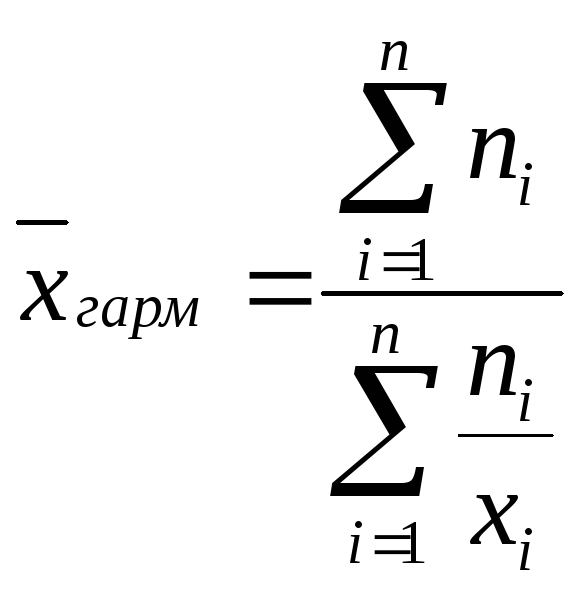
4.4. Средняя квадратическая используется тогда, когда варианта представляет размерность второго порядка, например, когда х_i есть площадь поверхности, полученная измерением длин сторон прямо- угольника. В этом случае используется формула

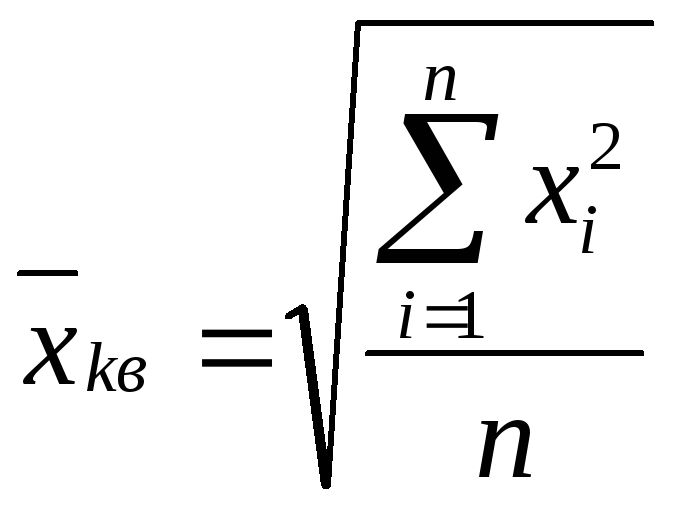
5.5. Медиана делит ранжированный ряд распределения вариант х_i на две равные части. Таким образом, в ранжированном ряду распределения одна половина ряда имеет значения признака, превышающие медиану, а другая — меньше медианы. Медиана является характеристикой центральной тенденции признака, особенно когда концы распределения расплывчаты и неясны.

5.6. Мода показывает значение величины х_i, имеющей наибольшую частоту в статическом ряду распределения. Так, в табл. 3.1 и на рис. 3.1 показано, что мода равна хт = 1 при частоте т_i = 10.

4.7. Выборочная дисперсия

Среднее квадратическое отклонение .

4.8. Дисперсия альтернативного признака используется тогда, когда признак измеряется двумя альтернативными значениями, например 0 и 1, да и нет, присутствует или не присутствует. Доля элементов выборки, обладающих признаком 1, равна .

признаком 0

Средняя

Дисперсия

Интервальные оценки параметров распределения случайных вели- чин. Точечные оценки параметров не дают информации о степени близости оценки Θ_b к соответствующему теоретическому параметру

Θ. Поэтому более информативный способ оценки неизвестных пара- метров состоит не в определении единичного точечного значения, а в построении интервала, в котором с заданной степенью достоверности окажется оцениваемый параметр, т.е. в построении так называемой интервальной оценки параметра Θ.

Интервальной оценкой параметра Θ называется интервал, границы которого Θ_b1 и Θ_b2 являются функциями выборочных значений х₁, х₂, ... х_n и который с заданной вероятностью накрывает оцениваемый параметр Θ

где α - уровень значимости.

Интервал (Θ_b1, Θ_b2) называется доверительным, его границы Θ_b1

иΘ_b1 являющиеся случайными величинами, соответственно нижним и верхним доверительными пределами. Любая интервальная оценка может быть охарактеризована совокупностью двух чисел: шириной доверительного интервала Н = Θ_b1 - Θ_b2, являющейся мерой точности оценивания параметра Θ, и доверительной вероятностью у, характеризующей степень достоверности (надежности) результатов, Чаще всего в расчетах используется величина у равная 0,9; 0,95 и реже 0,8; 0,85; 0,99; 0,999.

Общая процедура получения интервальной оценки состоит в следующем:

1. Записывают определенное вероятное утверждение вида

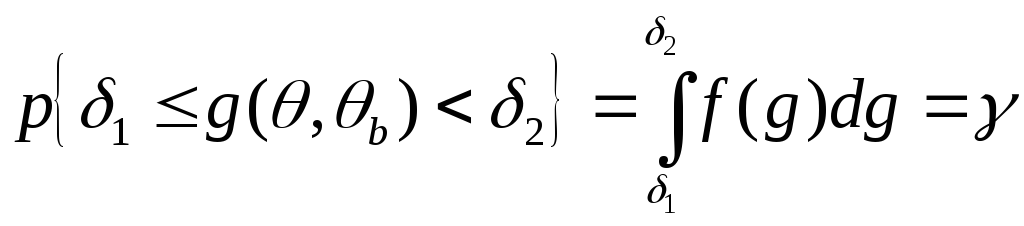
где f(g) — функция распределения плотности вероятностей случайной величины g. При этом значения δ₁ и δ₂ определяют обычно с учетом дополнительных условий

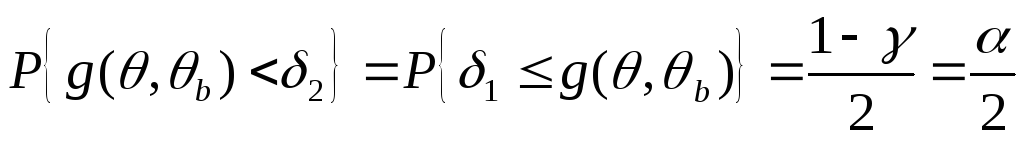
2. Аргумент g преобразуют так, чтобы в окончательном виде оцениваемый параметр оказался заключенным между величинами, определяемыми по выборке. Это и будут границы доверительного интервала (Θ_b1, Θ_b2). Функцию g(Θ, Θ_b2) выбирают таким образом, чтобы она допускала подобное преобразование и имела известную (лучше табулированную) функцию плотности вероятностей f(g). Последнее обстоятельство существенно упрощает определение значений δ₁ и δ₂.

В качестве примера получим интервальную оценку математи- ческого ожидания М(х) нормальной генеральной совокупности с известной дисперсией D(x). Известно, что функция

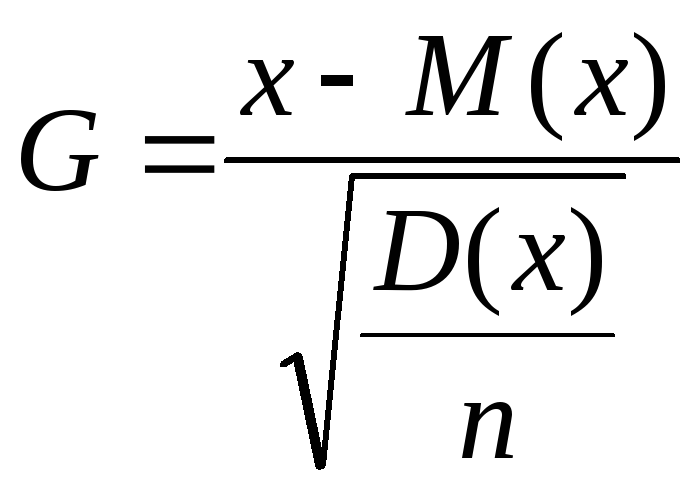
подчиняется нормированному нормальному распределению

(см. приложение 1). Тогда можно записать:

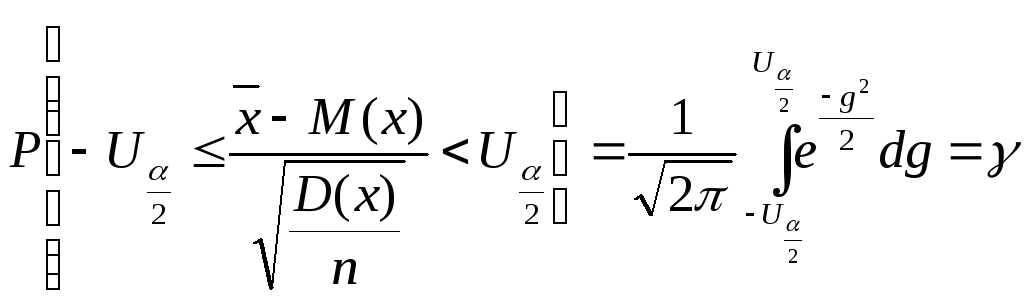
После преобразования аргумента получим:

Следовательно, для данного случая:

а ширина доверительного интервала

Для нормально распределенной случайной величины доверительный интервал определяется по формулам:

• если теоретическое значение дисперсии неизвестно, то для математического ожидания доверительный интервал будет иметь вид:

где k — число степеней свободы, k = n - 1;

t_a,k — табличное значение критерия Стьюдента, определяемое по таблице, приведенной в приложении 2;

• для теоретической дисперсии

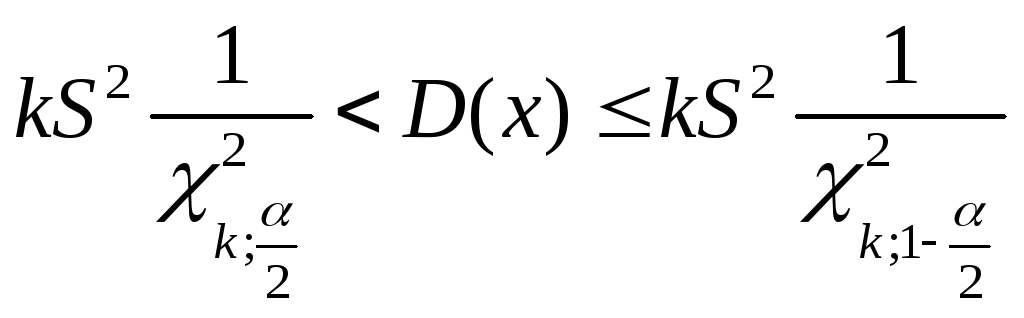
где k = n – 1, χ ²_{k;α /2}, χ ²_{k;1-α /2} - нижнее и верхнее значения критерия

Пирсона при заданных k и α/2, определяемое по таблице, приведенной в приложении 3.

Используя интервальные оценки, можно определить объем выборки, задаваясь точностью оценки. Если оценивается математическое ожидание, то точность оценки будет равна

При заданном значении δ и D(x) объем испытаний будет равен

При неизвестном D(x) объем испытаний определяется по фор- муле

Если оценивать дисперсию D(x), то, задаваясь значением δ_g, можно использовать уравнение

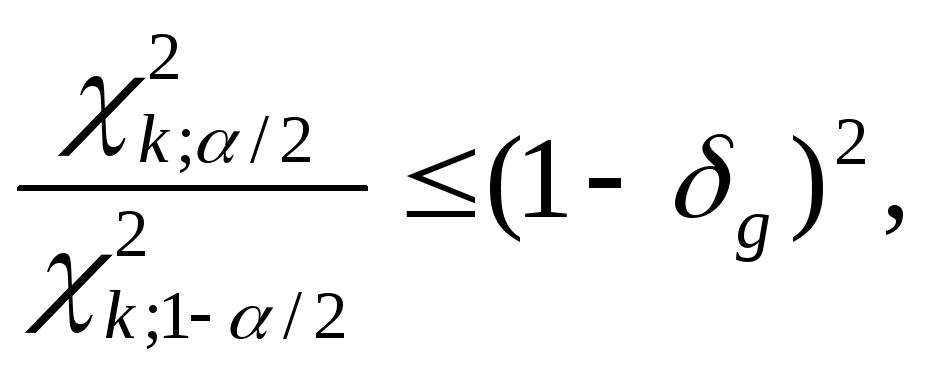
затем с помощью таблиц χ ² распределения (см. приложение 3) подо- брать такое соотношение в левой части неравенства, чтобы оно удовлетворяло правую часть, и затем определить объем испытаний n = k+L.

Доверительный интервал для генеральной доли P устанавливается по формуле

где P_b — выборочная доля;

U_a/2 — критерий, выбираемый по таблице (см. приложение 4, при U_a/2= x).

Величина U_a/2, вычисляется по формуле

Откуда

где S_pf – ошибка выборочной доли.

Если вместо доли в качестве оценки генерального параметра используется процентная частота, то ее ошибка вычисляется по формуле

Границы доверительного интервала p+UpS ~ для генеральной доли устанавливаются с достаточной точностью в тех случаях, когда выборочные доли равны или не сильно отклоняются от 50% численности групп. Если же выборочные доли не равны (75% < р < 25%) и тем более близки к нулю и единице, довери- тельные границы для генеральной доли следует определять с по- мощью вспомогательной величины < р,

Эта величина, предложенная Р.Фишером, имеет распределение, близкое к нормальному. Ее параметром служит выборочная ошибка, равная .

Значения φ зависят только от р.

Для практического использования этой величины служит таблица, приведенная в приложении 5, в которой содержатся значения φ для разных значений доли р, выраженной в процентах.

Пример. Из общего числа 5800 чел., проживающих в населен- ном пункте, методом случайного отбора обследовано 1500 лиц, среди которых обнаружено 200 больных.

Доля больных

или 13%

Ошибка доли

или 8%

Для доверительной вероятности γ=0,9 величина U_α/2=1,96=2. Тогда доверительный интервал

Отсюда с вероятностью 0,90 следует заключить, что генеральная доля находится между Р_верх. = 0,15 и Р_ниж. = 0,11. Так как генеральная доля меньше 25%, исправим доверительный интервал с по- мощью величины rp. Для доли больных

для Р%=13,0025 величина φ > 0,738 (см. приложение 5). Определим S_pf

Отсюда границы для доверительного интервала р равны:

• нижняя 0,738 — 2 х 0,07 = 0,601;

• верхняя 0,738+ 2 х0,07 = 0 875.

Переводим значения р в исходные величины по таблице (см. приложение 5): = 8,8% и =18,0%. Это значит, что с вероятностью Р = 0,90 можно утверждать, что доля больных в населенном пункте при данных условиях не должна выйти за пределы 8,8% — 18% от общего числа жителей.