Файл: Математическое моделирование в экологии.doc

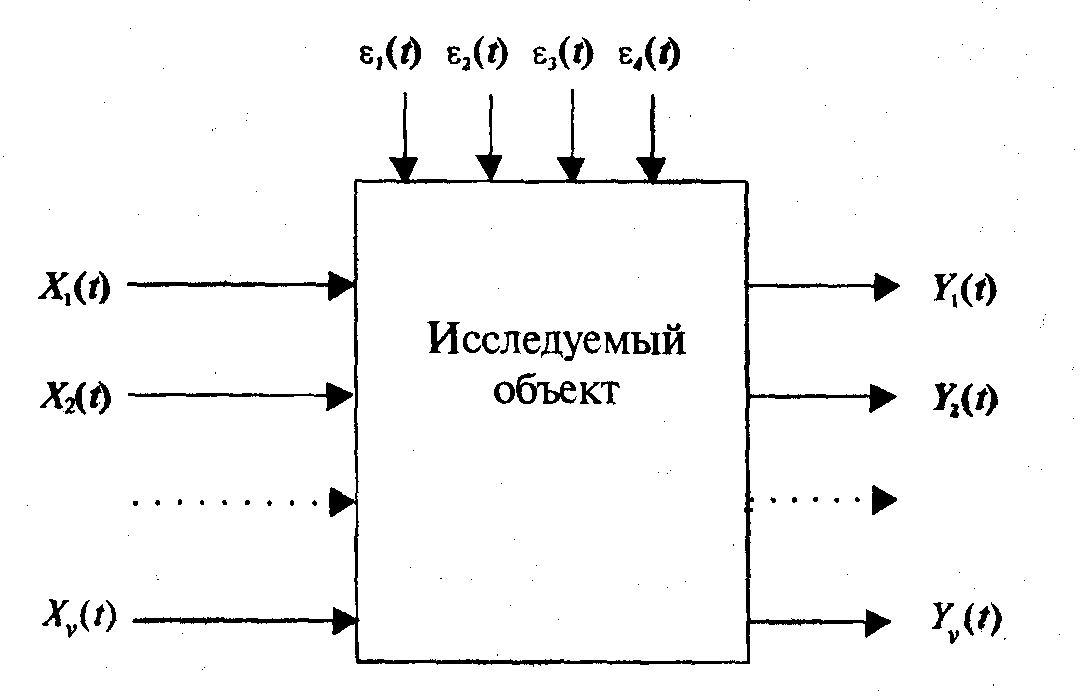
Рис. 13.10. Схема многомерного процесса.

Запись в матричной форме имеет вид:

(13.29)(5.29)

где

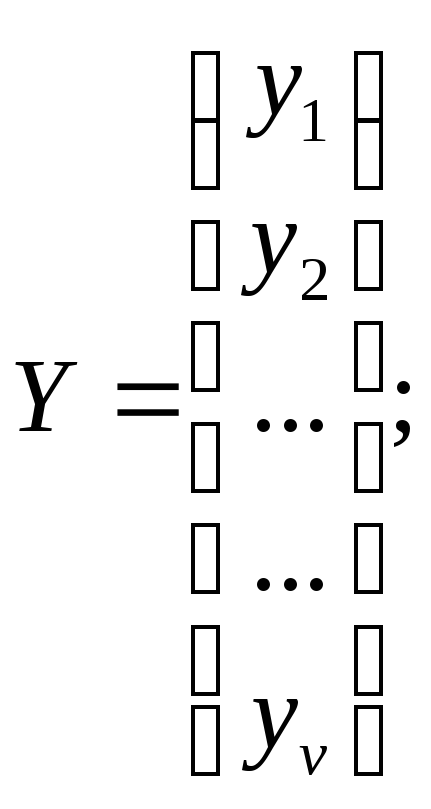
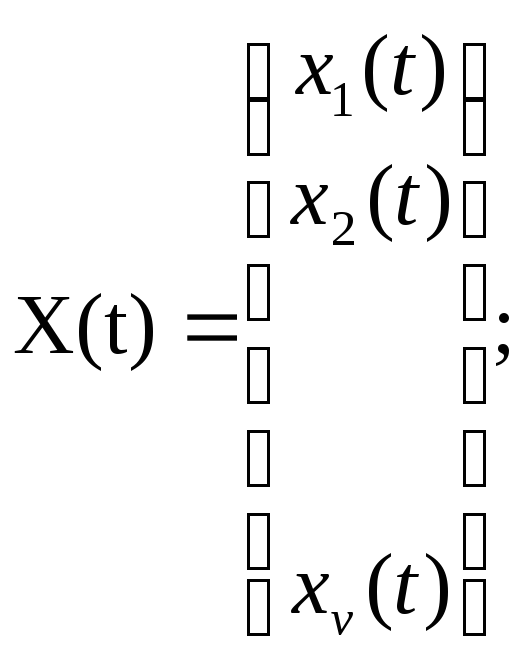
Предположим, что смесь в смесителе содержит три (см. рис. 5.8) компонента, вступающих в реакцию по схеме

k₁ k₂

АВ С

где k_i — константы скоростей реакций. Тогда система уравнений и конкретные начальные условия в уравнении (5.29) примут вид

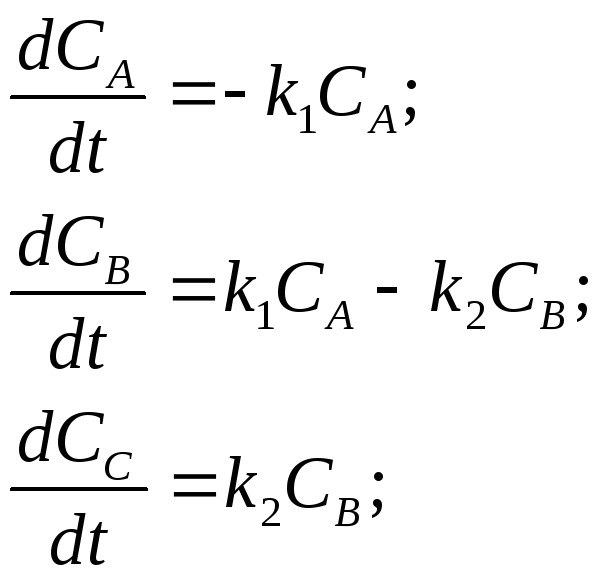
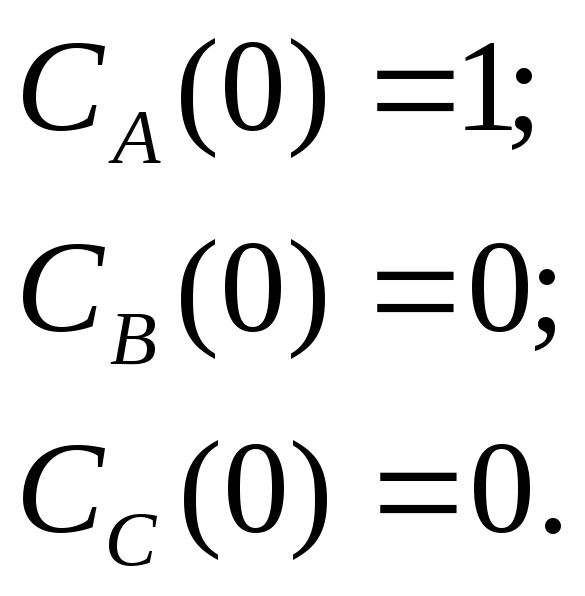
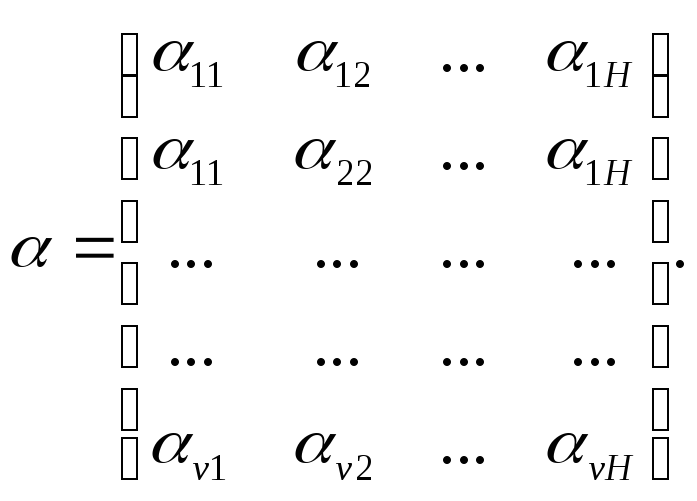
Пусть матрица X(t) задана априори, а величины Y₀, и а требуется

оценить во временном интервале 0 < t < t_n пo дискретным наблюдениям, представленным следующим соотношением

Y(t₁) =h(t₁) y(t₁)+ ε(t₁), , (13.30)(5.30)

где Y(t₁) — вектор-столбец n1;

h(t₁) — матрица nv, заданная априори; е(t₁) — вектор -столбец n1 (вектор "шума"), элементами которого яв- ляются ненаблюдаемые ошибки.

Решение модели (5.28) можно записать в форме

(5.31)

Например, решение модели с тремя химическими компонента- ми в смесителе имеет вид

Подстановка решения (5.31) в соотношение (5.30) дает:

.

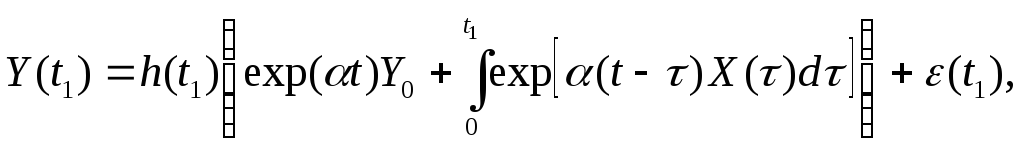что можно представить в общей форме

.

Подобное выражение можно записать и для непрерывных наблюдений, просто опуская индекс i при t. Модель, содержащая одно или несколько линейных дифференциальных уравнений более высокого порядка с постоянными коэффициентами, можно преобразовать в модель, содержащую систему обыкновенных дифференциальных уравнений первого порядка.

При оценке случайных процессов в экологии большое значение играют выбросы за определенные значения времени и оценка их вероятности.

Пусть имеется случайный процесс Х(t) (рис.5.11), где под длительностью выброса (t₀) понимается отрезок времени, в течение которого X(t) превышает заданный уровень Х₀. Представляет интерес длительность интервала t₀ между выбросами, т.е. отрезок времени, в течение которого X(t) не превышает уровня Х₀.

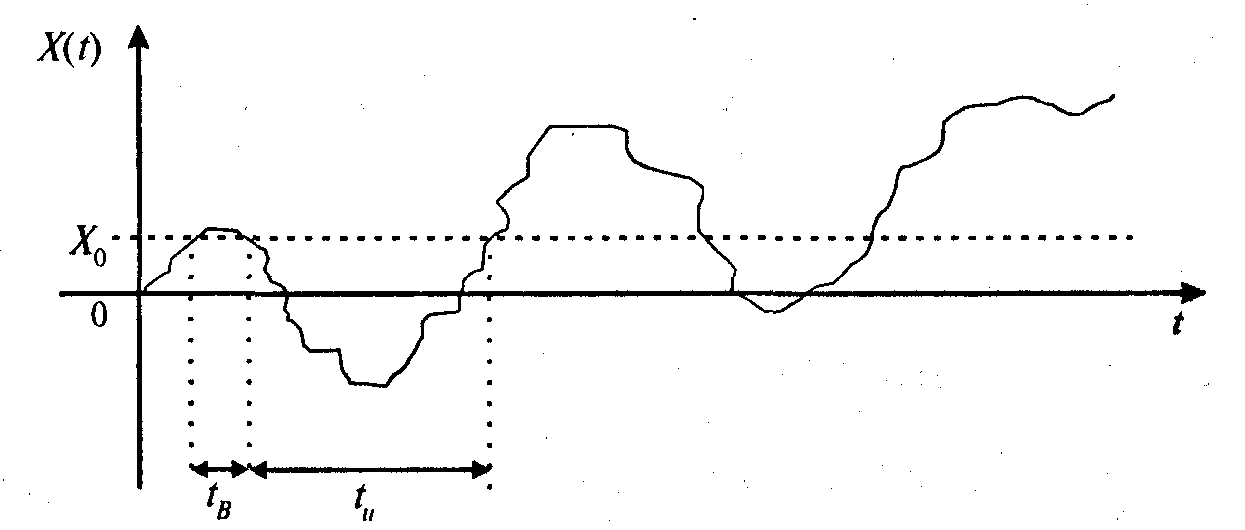
Рис. 13.11. Пересечение случайным процессом заданного уровня

Вероятность пересечения уровня Х₀ снизу вверх (т.е. с положительной производной) в достаточно малом интервале времени ∆t совпадает с вероятностью неравенств

х₀ — ∆х ≤ x(t) <х₀

Пусть ω₂(х, у, t) — двумерная функция распределения X(t) и в совпадающий момент времени t.

Тогда

.

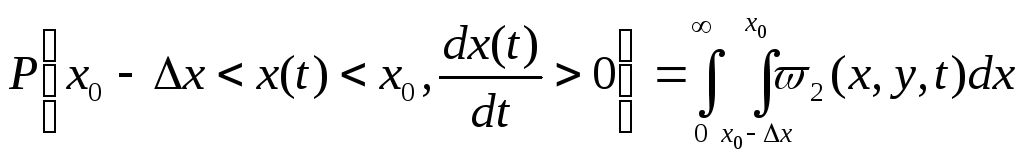При достаточно малом ∆t внутренний интервал можно заменить выражением

ω₂(x₀,y,t) ∆x = y ω₂(x₀,y,t) ∆t

и тогда получим выражение

(5.32)

где

(5.33)

Рассмотрим интервал времени конечной длины (t, t +T) и разобьем его на N не перекрывающиеся малые интервалы (t_i, t_i +∆t_i) с промежуточными точками t=t₁< t₂ < ... <t_N+i; ∆t_i= t_i+1 - t_i.

Для каждого из указанных интервалов времени определим случайную величину v_i равную 1, если X(t) на интерва- ле (t_i, t_i+∆t_i) пересекает уровень х₀ с положительной производ- ной, и, равную нулю, если такого пересечения не происходит. Эти случайные величины являются своеобразными счетчиками пересечений. Ясно, что общее число пересечений на интервале (t, t+T) равно:

Предполагается, что ∆t_i столь мало, что вероятностью более одного пересечения в это время можно пренебречь. Так как вероятность того, что v_i =1, определяется по формуле (5.32), то среднее значение М₁(х₀, t, T) числа пересечений с положительной производной уровня х₀ на указанном интервале равно:

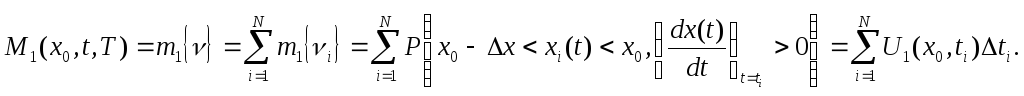
Переходя к пределу при N→∞, находим следующую формулу для среднего числа пересечений уровня x₀ с положительной производной на интервале (t, t+T)

или

,

Среднее значение числа пересечений уровня х₀ с положительной производной уровня х₀ в единицу времени (т.е.) равно:

.

Если случайный процесс стационарен, то

.

Заметим, что среднее число пересечений с заданным знаком производной совпадает с числом выбросов случайного процесса.

Для стационарного случайного процесса дисперсия числа пе- ресечений с положительной производной уровня х₀ в единицу времени равна:

. (5.34)

Очевидно, что формула (5.34) определяет также и дисперсию числа выбросов на заданном интервале в единицу времени соответственно. Если задана одномерная функция распределения случайного процесса — F₁(х), то среднее значение длительности выбросов равно:

назад

Лекция 14. Балансовые модели.

Национальное хозяйство развивается в сложной сети межотраслевых взаимосвязей, понять которые во всей их совокупности путем простого суммирования невозможно. Например, спрос на металл оказывает влияние на добычу железной руды и руд, содержащих различные металлы и вещества, необходимые для получения стали и сплавов. Это в свою очередь увеличивает спрос на горнорудную технику. Обычные методы счета не пригодны для количественного анализа прямого и косвенного эффектов распространения таких влияний одной отрасли на другую. Решить проблему можно только с помощью современных методов анализа, в основе которых заложен метод межотраслевого баланса («затраты — вы- пуск»). Этот метод разработан В. Леонтьевым. Он позволяет дать последовательные и численно определенные ответы на вопросы, связанные с межотраслевыми взаимодействиями и их влиянием на современные макроэкономические показатели. Метод межотраслевого баланса оказался пригоден для решения целого класса экологических задач, связанных с расходами и пополнениями экологических ресурсов.

Рассмотрим математическую модель рационального использования природных ресурсов в процессе промышленного производства, в котором используется модель межотраслевого баланса.

Сферу жизнедеятельности человека составляют семь основных экологических подсистем: космос, солнечная энергия, атмосфера, почва, леса, вода, недра Земли, каждая из которых характеризуются определенными параметрами ,запасами ресурсов ,их расходом за период от t₀ до t и восполнением за этот же период.

Введём понятие «экологическое равновесие» для подсистем, которое определяется условием сохранения запаса ресурсов и их параметрами, обеспечивающими жизнедеятельность человека и сохранность других экологических подсистем региона, что может быть представлено в виде неравенств: