Файл: Математическое моделирование в экологии.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 31.03.2024

Просмотров: 1169

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Конспект лекций

Владикавказ

Математическое моделирование элементов сложных экологических систем

Лекция 1. Введение в моделирование. Исторический экскурс.

1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии

Лекция 2.

2.1. Элементы моделирования

2.2. Этапы построения математической модели

1.4. Элементы теории подобия, применяемые в моделировании

Лекция 3

3.2. Экологические модели

3.2.1. Основы экологометрики

3.2.2. Выборочный метод в экологометрике.

Зависимость числа интервалов от объема выборки

Статистический ряд по интервалам

Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам

4.4. Статистические оценки гипотез об экологических моделях

Определение вариантов выборок

Выборка из генеральной совокупности

Статистическая таблица

Лекция 5.

Результаты эксперимента

Статистическая таблица эксперимента

Пример преобразования членов уравнения регрессии

Вычисление данных для линеаризации уравнения регрессии

Нормальные уравнения мнк для некоторых функций

Статистическое оценивание уравнения регрессии и парной корреляции.

Обработка результатов наблюдений

Лекция 6.

Рекомендации по выбору вида функции

3.4. Динамические статистические модели

Посадка леса

Данные по объему сброса качественных сточных вод

Данные по объему сброса сточных вод за 5-летие

Пример расчета 5-летних средних

Условное обозначение времени

Расчетные значения для определения уравнения динамики

Ряд динамики для определения сезонных колебаний

Лекция 7. Многофакторные эколого-математические модели. Анализ влияния отдельных факторов в экологической модели.

Эксперименталъный материал исследования

Результаты проведенных опытов

8.1. Анализ влияния отдельных факторов в экологической модели.

Лекция 9. Методы оптимизации. Метод Лагранжа

Лекция 10. Метод линейного программирования.

Лекция 11. Функциональные модели.

Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.

Численные ошибки использованных для вычисления данных

Лекция 13. Статистические модели динамики.

Лекция 14. Балансовые модели.

Лекция 15.

Лекция 16. Информационные технологии в экологии. Экологические информационные системы.

1 6.1. Экологические информационные системы

1. Какова область значения для числовых характеристик?

Лекция 17. Использование информационных технологий для решения задач экологии.

Специальные приложения.

Значение функции

Значение критерия

Значение критерия

Критические значения коэффициента корреляции rk;α

2. Основы теории подобия

2.1. Подобие физических явлений и его признаки

2.2. Анализ размерностей

2.3. Первая теорема подобия

2.4. Применение методов подобия в математическом

11.3. Численные методы решения дифференциальных уравнений

11.3.1. Постановка задачи

11.3.2. Процесс численного решения

11.3.3. Метод Эйлера

11.3.4. Модифицированный метод Эйлера

11.3.5. Метод Рунге – Кутта

11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений

11.3.7. Общая характеристика одношаговых методов

3.8. Многошаговые методы

11.3.9. Методы прогноза и коррекции

11.3.10. Краткая характеристика методов прогноза и коррекции.

11.3.11. Выбор шага и погрешность решения.

11.3.12. Жесткие задачи

11.4. Имитационное моделирование систем

11.4.1. Принципы имитационного моделирования

11.4.2. Объекты моделирования

11.4.3. Динамическая модель исследуемого объекта

11.4.4. Построение имитационных моделей динамических систем

11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши

11.4.6. Синтез имитационной модели на основе структурной схемы

11.5. Теоретические основы построения математических моделей систем

11.5.1. Компонентные и топологические уравнения

11.5.2. Компонентные и топологические уравнения механической системы

11.5.3. Компонентные и топологические уравнения электрической системы

11.5.4. Компонентные и топологические уравнения гидравлической системы

11.5.5. Компонентные и топологические уравнения тепловой системы

11.6. Метод электроаналогий

11.6.1. Сущность метода электроаналогий.

11.6.2. Электромеханические аналогии

11.6.3. Построение имитационных моделей методом электроаналогий

11.6.4. Плоское прямолинейное движение звеньев

11.6.5. Электрогидравлические аналогии

11.6.6. Электротепловые аналогии

Литература

Общий запас ресурса и его параметров

.

Оценка запаса ресурса и его параметров в момент времени t есть оперативный запас, который равен:

.

В процессе жизнедеятельности за период Т человек потребляет в среднем единицресурса наличное потребление и единиц ресурса на производственные нужды. Тогда общая потребность в ресурсах за период Т будет равна:

где N — средняя численность населения региона в период Т.

В качестве условий экологического равновесия подсистемы можно записать:

.

при условии .

С другой стороны, желательно, чтобы расход ресурса пополнялся, т.е.:

Личное потребление всех видов ресурсов за время T.

,

где n — число видов ресурсов в личном потреблении.

Потребление за единицу времени

.

При приращении личного потребления i-го ресурса на величину за время ∆t, предельный расход по каждому из и ресурсов будет равен:

,

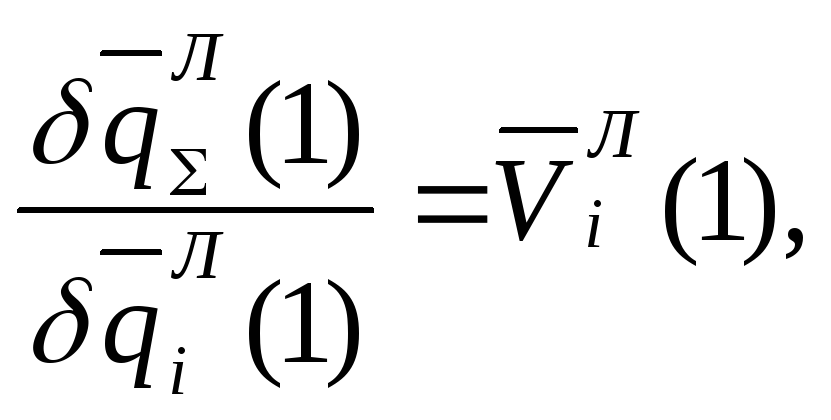
т.е. скорости расхода i-го ресурса Vi.

Соответственно, для расхода ресурсов на производственные нужды:

;

;

,

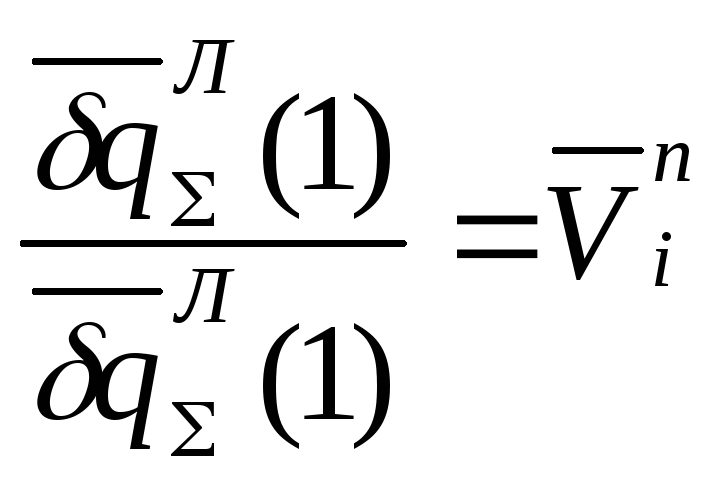Изменение параметра bj () i- го ресурса () при личном

потреблении за время Т равно за единицу времени — Суммарное потребление по параметрам i-го ресурса

.

Суммарное потребление по параметрам всех видов ресурсов

В качестве условий экологического равновесия подсистемы можно записать:

.

при условии .

С другой стороны, желательно, чтобы расход ресурса пополнялся, т.е.:

.

Личное потребление всех видов ресурсов за время Т:

q (Т)=q,""(Т)+ц,"(Т)+...+q„(T),

где n — число видов ресурсов в личном потреблении.

Потребление за единицу времени

При приращении личного потребления i-го ресурса на величину за время ∆t, предельный расход по каждому из и ресурсов будет равен:

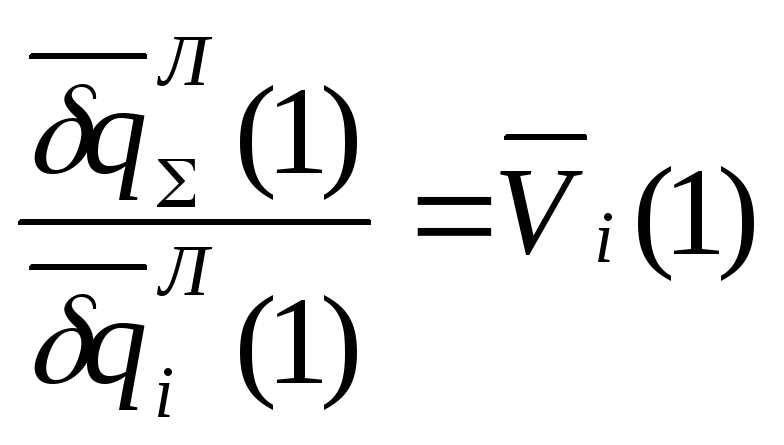, i=.

т.е. скорости расхода i-го ресурса Vi,

Соответственно, для расхода ресурсов на производственные нужды:

;

i=.

Изменение параметра bj (j' = ) i-го ресурса (i = ) при личном потреблении за время Т равно за единицу времени — Суммарное потребление по параметрам i-го ресурса –

.

Суммарное потребление по параметрам всех видов ресурсов

. (5.35)

Функция личного потребления ресурсов

, (5.36)

характеризует влияние личности на потребление ресурсов и изменение их параметров в процессе жизнедеятельности.

При потреблении ресурсов для производственных нужд по параметрам, аналогично формулам (5.35) и (5.36), запишем

.

Производственная функция

характеризует влияние производственной (и иной подобной деятельности) на потребление ресурсов и изменение их параметров в процессе производства.

Таким образом, потребление ресурсов можно представить в виде матриц:

а) суммарного потребления ресурсов:

на личное потребление

, i=.;

производственное потребление

i=.

б) суммарное потребление ресурсов по параметрам:

личное потребление

, i=, i=.

производственное потребление

i=, i=.

Общее потребление ресурсов в единицу времени

,

Общая функция потребления

характеризует влияние личной и производственной деятельности на экологическую систему в целом на данном этапе существования региона (общества, проживающего в данном регионе).

Экономический механизм использования природных ресурсов из условия «экологического равновесия» может быть представлен в виде условий для периода времени Т (от t1 до t2).

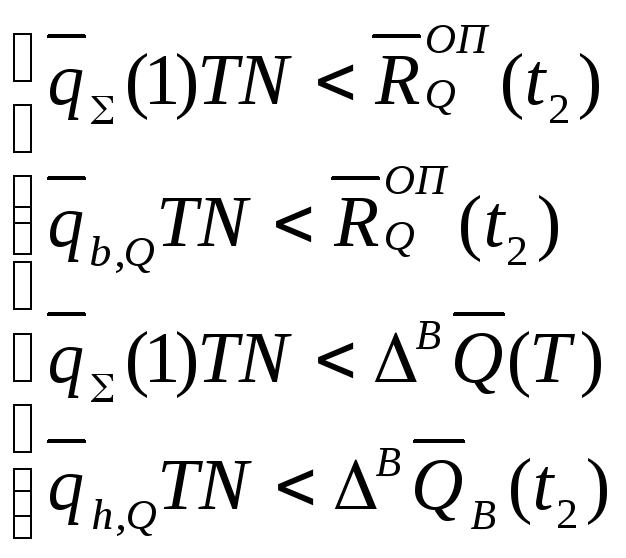
при условии

,

где — запас ресурсов к концу периода Т;

—восстановление параметров ресурсов к концу периода Т.

Из условия максимального уровня жизни на данный период функция полезности

.

Стоимость единицы ресурса при потреблении обозначим по параметру bi –. Стоимость единицы ресурса при восстановлении (пополнении) – ;по параметру bi —. Стоимость расхода ресурсов есть функция запаса ресурсов

= f(RQ),

изменяющаяся в зависимости от исчерпываемости и восстанавливаемости запасов. Графики функций представлены на рис. 14.12. Отсюда видно, что стоимость ресурса возрастает с убыванием его запаса.

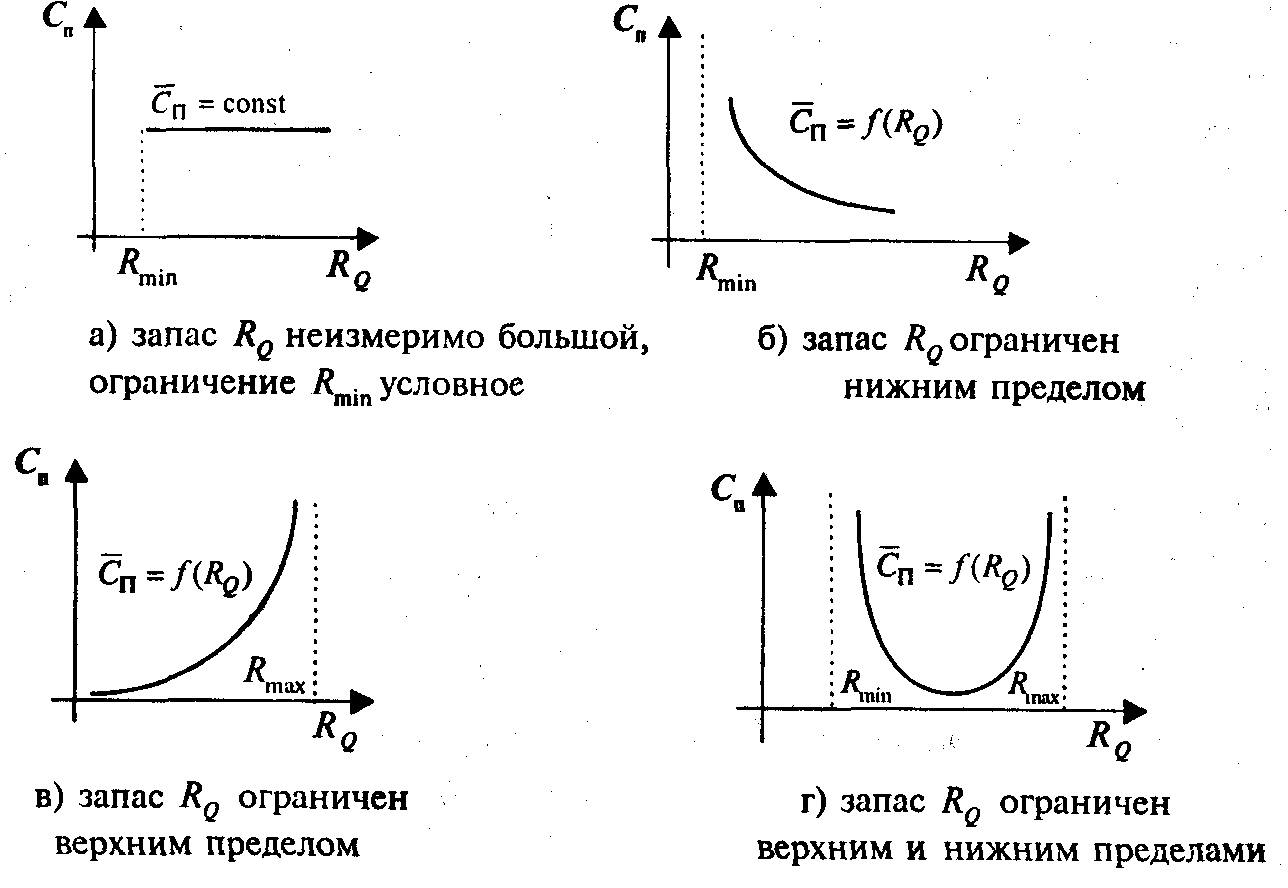
Рис. 14.12. Графики стоимости ресурсов в зависимости от их запасов

Стоимость восстановления ресурсов зависит от капитальных зат- рат (Кв) и затрат труда (LB), т.е.

,

а также от выбора технологий восстановления, при условии

С точки зрения общественной целесообразности желательно, чтобы цены и были минимальны, а цена ,кроме того, была бы не настолько велика, чтобы можно было организовать воспроизводство ресурса.

Следует учесть, что при восстановлении i-гo ресурса часто требуется затратить часть других видов ресурса, в свою очередь требующих восстановления. Если в регионе имеется k видов ресурсов (j = ) и n производственных потребителей этих ресурсов (i =), то расход зависит от объема выпускаемой продукции каждым из этих потребителей.

Пусть общий объем выпускаемой продукции первым предприятием , складываетсяиз продукции, удовлетворяющей спрос других производителей, у которых она используется для производства собственной продукции и продукции конечного спроса, поступаю- щей на рынок, т.е.

, i=,

где –объем выпускаемой продукции первым предприятием, который потребляется i-ым предприятием для выпуска своей продукции. Тогда общий объем выпускаемой продукции в регионе равен:

Смотрите также файлы