Файл: Математическое моделирование в экологии.doc

или в матричной форме, с учетом матрицы коэффициентов прямых затрат А с элементами:

, ,

и мультипликатора Леонтьева В = (1 — А)^-1, объем выпускаемой продукции по региону составит

Х = (l — А)^-1F,

или

Х= ВF.

где l — единичная матрица размером пп;

В — матрица коэффициентов полных затрат при выпуске продукции. Пусть каждый i-й потребитель использует i-й ресурс в количестве q_il на единицу выпускаемой продукции. Матрица удельных расходов будет иметь вид:

тогда расход ресурсов по региону равен:

Q=X^TxG=(X₁, X₁, …., X₁)x=(Q₁, Q₂, …., Q_n),

где Q_i — общий расход i-го ресурса по региону l = .

При стоимости единицы ресурса с₁, с₂, ..., с_l, ..., с_k общая стои- мость потребляемых ресурсов будет равна:

, или .

Обозначим общий объем l-го ресурса в регионе через R₁, а до- пустимый расход ресурса — . В случае, если

,

то стоимость единицы ресурса остается постоянной. Если имеет место дефицит ресурса, т.е. когда

или (5.37)

стоимость ресурса возрастает с ростом дефицита .

Допустим, что «экологическое равновесие» в регионе определяется условием

Q≤R^D

В этом случае основная задача экологической системы состоит в контроле условия (5.32), которое для каждого ресурса можно за- писать в виде

,

где — запас l-го ресурса.

В случае дефицита l-ro ресурса требуется уменьшение объема выпускаемой продукции, для которой необходим этот ресурс. Та- ким образом, задача становится задачей выбора решения: либо работать с дефицитом природного ресурса, либо уменьшить объём выпускаемой продукции. В более общем виде эта задача сводится к минимизации потерь региона, которую мы и рассмотрим.

Пусть система имеет начальное состояние S₀ удовлетворяющее по всем видам ресурсов условиям «экологического равновесия» 5.32. Из состояния S₀ система может переходить в состояния S₁, S₂,..., S_n, каждое из которых характеризуется дефицитом при- родных ресурсов и соответствующими объемами производства.

Если система находится в состоянии S_i, то мы имеем множество D(S) различных допустимых решений о минимизации в этом состоя- нии. Ожидаемые экономические потери, обусловленные решением dD(S), в состоянии системы S_i. обозначим через R(S_i, d_i)

После того как принято решение d_i из множества возможных D(S_i), система переходит из состояния S_i, в состояние S_i+1. Вероятность перехода из S_i в S_i+1, равна p(S_i→S_i+1, d_i). Экономические потери от нового состояния R(S_i→S_i+1, d_i). Тогда ожидаемые потери от дефицита ресурсов и увеличения объема выпускаемой продукции ∆Х будут определяться условиями

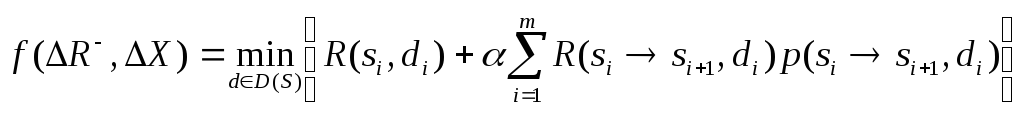
назад

Лекция 15.

Балансовые модели (продолжение)

для каждого s S, 0 < α < 1 (α — риск), где f(∆R^-, ∆X) — ожидаемые потери, определяемые оптимальной стратегией на бесконечном плановом периоде при заданном текущем состоянии S.

математического программирования.

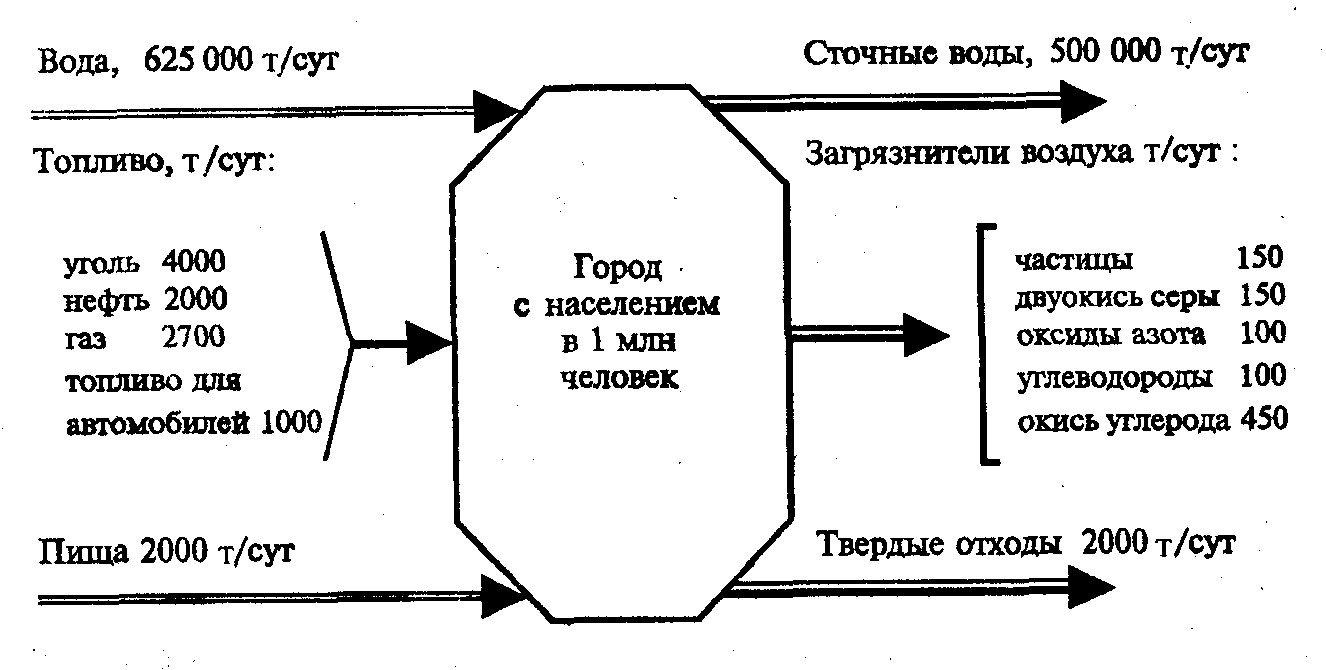
Рис. 15. 13. Схема материальных потоков

В другом случае используется модель межотраслевого баланса с учетом затрат на ликвидацию загрязнений. Здесь применяется модель Леонтьева — Форда.

Модель показывает, каким образом материальные потоки, поступающие в экономико-экологическую систему, распределяются затем по разным видам деятельности. Все, что поступает в систему в виде сырья и материалов, либо преобразуется в готовые изделия, либо идет в отходы производства. Представление об объемах материальных потоков, поступающих в окружающую среду, дает следующая условная схема (рис. 15.13), составленная для города с населением в 1 млн. человек. На схеме дано изображение трех основных входных потоков (вода, пища и топливо) и трех выходных потоков (сточные воды, твердые отходы и загрязнения воздуха), которые являются общими для всех городов. В этой модели появляются величины, измеренные в натуральных единицах, а именно отходы производства по каждому виду загрязнителей. Это обстоятельство существенно меняет привычные свойства модели межотраслевого баланса, в которой все величины выражены в стоимостной форме.

Основные условия модели Леонтьева — Форда в матрично-векторной форме можно записать следующим образом

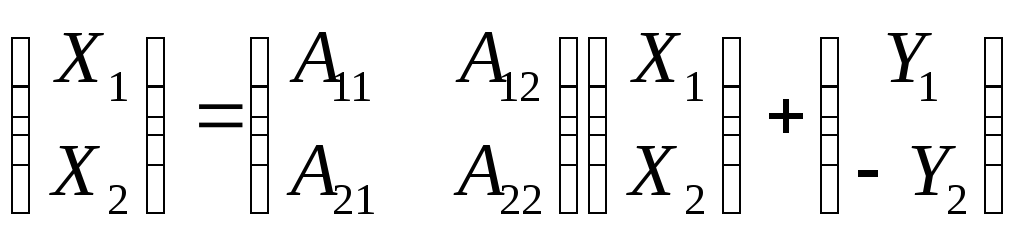, (5.38)

где Х₁ - вектор валовых выпусков продукции размерности т,

Х₂ - вектор объемов загрязнений, подлежащих ликвидации, размерности n - т,

, ;

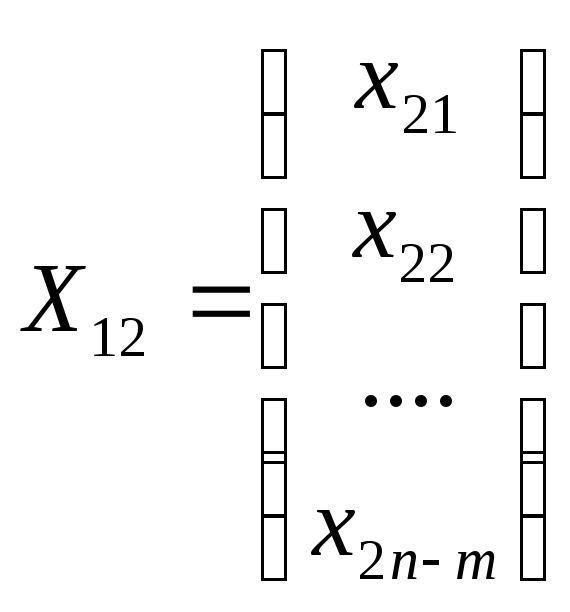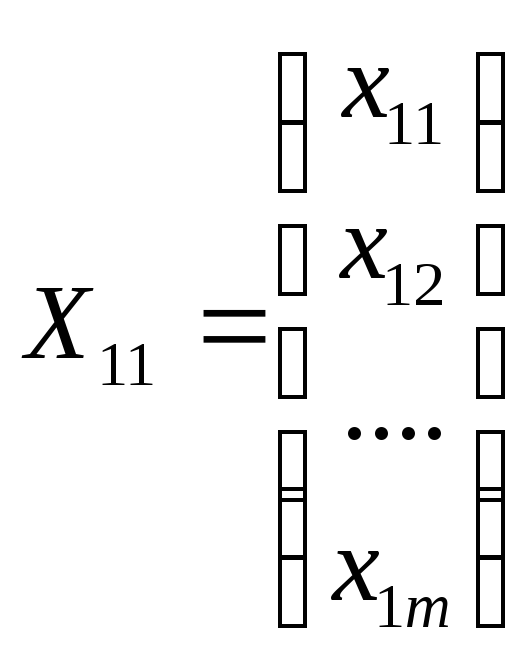
Y₁ — вектор конечной продукции размерности n;

Y₂— вектор объемов загрязнений, которые в настоящее время не могут быть ликвидированы (например, из-за нехватки средств), размерности n - т,

, ;

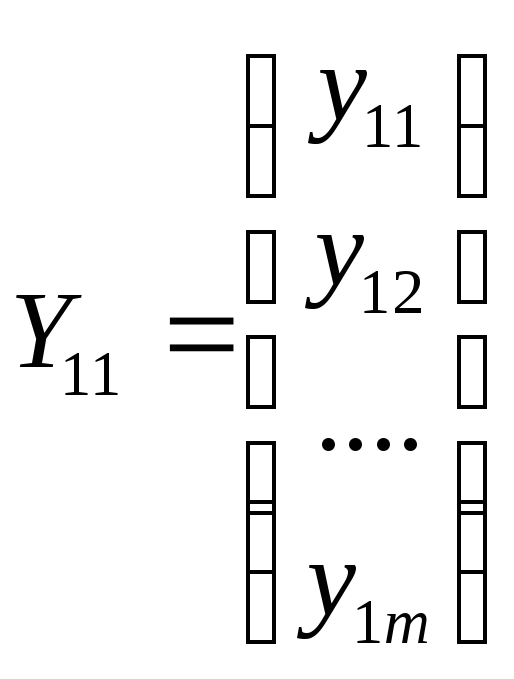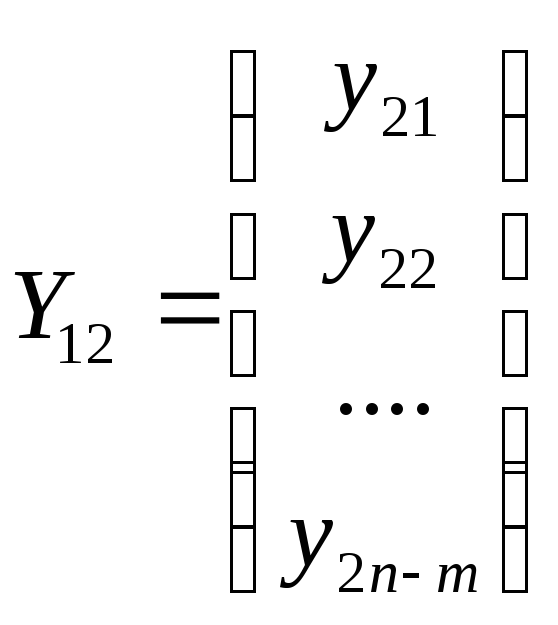А₁₁= (а_ij)_n-m — матрица прямых затрат (матрица А в первоначальной модели межотраслевого баланса, которая имеет вид

где а_ij, — определяет какой объем i-гo ресурса необходим для производства единицы продукции j-й отрасли);

А₁₂=(а_iq)_m(n-m) — матрица прямых затрат продукта i на уничто- жение единицы загрязнения вида q,

А₂₁=(а_ki)_m(n-m) — матрица коэффициентов, характеризующих количество поступающих в окружающую среду отходов по каждо- му виду загрязнителей k в расчете на единицу валового выпуска продукции j каждой из отраслей;

А₂₂=(а_kq)_(n-m)(n-m)— матрица коэффициентов выброса загряз- нений k-гo вида при уничтожении единицы загрязнения вида q, т.е. учитывает вторичный эффект загрязнений.

Перепишем модель Леонтьева — Форда (5.38) в виде:

X₁=A₁₁X₁+A₁₂X₂+Y₁; (5.39)

X₂=A₂₁X₁+A₂₂X₂+Y₂. (5.40)

С помощью этой модели может быть решена задача определе- ния валовых выпусков продукции отраслей с учетом затрат на лик- видацию загрязнений, которая была ранее описана, но лишь с пред- положением, что отходы по каждому виду загрязнителей пропорци- ональны валовым выпускам продукции отраслей, а затраты на лик- видацию загрязнений пропорциональны объемам загрязнений, под- лежащих ликвидации. В этой модели учтены только производственные загрязнения A₁₂ и вторичные загрязнения А₂₂. Вектор Х₂+Y₂ характеризует общие объемы отходов по каждому виду загрязне- ний, образовавшихся в течение года в результате производственной деятельности. Загрязнения, которые образуются в сфере конечного потребления, могут быть отражены в модели также, как это сделано для производственных загрязнений. В системе уравнений (5.39 - 5.40) неизвестными являются вектор валовых выпусков продукции отраслей Х₁ и вектор подлежащих ликвидации объемов загрязнений Х₂. Они могут быть найдены, если заданы вектор конечных выпусков продукции отраслей Y₁ и вектор объемов загрязнений, которые в на- стоящее время не могут быть ликвидированы Y₂. Но сразу по данной системе уравнений этого сделать нельзя. Преобразуем эту систему.

Если пренебречь вторичными загрязнениями, связанными с деятельностью предприятий, ликвидирующих загрязнения, т.е. если считать А₂₂ = 0, то получим:

X₁=A₁₁X₁+A₁₂X₂+Y₁;

X₂=A₂₁X₁+0 - Y₂.

Подставив в первое уравнение значение Х₂ получим:

X₁=A₁₁X₁+A₁₂(A₂₁X₁-Y₂)+Y₁;

X₁=A₁₁X₁+A₁₂A₂₁X₁-A₁₂Y₂+Y₁;

(I-A₁₁-A₁₂A₂₁)X₁ = -A₁₂Y₂+Y₁;

(I-A₁₁-A₁₂A₂₁)^-1(I-A₁₁-A₁₂A₂₁)X₁ = (I-A₁₁-A₁₂A₂₁)^-1(-A₁₂Y₂+Y₁).

Пусть В₁₁= (I - А₁₁ - А₁₂А₂₁)^-1 и В₁₂ = В₁₁А₁₂,

тогда

X₁ = B₁₁Y₁-B₁₂Y₂;

X₂ = A₂₁(B₁₁Y₁-B₁₂Y₂)-Y₂;

X₂=A₂₁B₁₁Y₁-(A₂₁B₁₂+I)Y₂.

Обозначим В₂₁ = А₂₁В₁₁ и В₂₂ = А₂₁В ₁₂+ I,

тогда

Х₂ = В₂₁Y₁ — В₂₂Y₂.

Итак, мы получили следующую систему уравнений:

X₁ = B₁₁Y₁ – B₁₂Y₂; (5.41)

X₂ = B₂₁Y₁ – B22Y₂. (5.42)

где для матриц В₁₁, В₁₂, В21 и В₂₂ имеем:

В₁₁= (I — А₁₁ — А₁₂А₂₁)^-1; В₁₂ = В₁₁А₁₂;

В₂₁ = А₂₁В₁₁; В₂₂ = А₂₁В₁₂ +I,

где

.

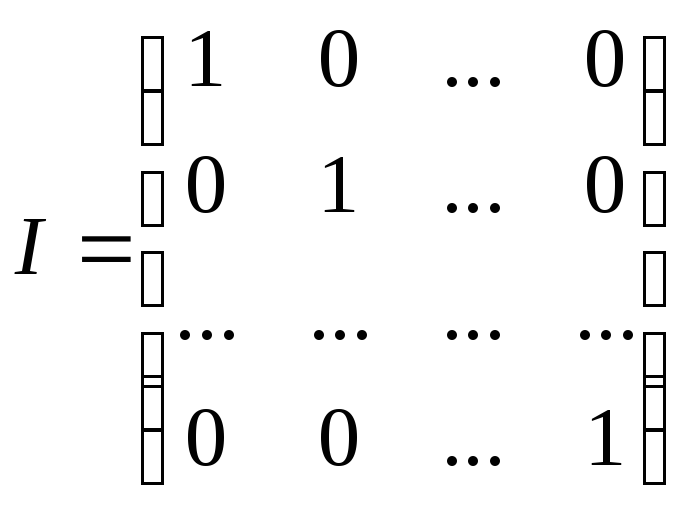В решении (5.41 — 5.42) вектор (В₁₁Y₁) характеризует валовые вы- пуски продукции отраслей при условии ликвидации всех загрязнений, образовавшихся в течение данного года в результате производственной деятельности (здесь и далее полагаем А₂₂ = 0). Иначе (В₁₁Y₁) — это вектор валовых выпусков продукции отраслей в случае, если бы все образующиеся в течение года загрязнения были бы ликвидированы; (В₁₂Y₂) — вектор потенциальных затрат промежуточной продукции. Промежуточная продукция — это часть всей продукции, представляющая закупки данного вида продукции отраслями-потребителями в качестве исходных материалов для производства их продукции на ликвидацию не ликвидируемых загрязнений. Этот вектор является частичной характеристикой обычно не учитываемых издержек производства. (B₂₁Y₁) — вектор потенциальных отходов производства в случае ликвидации всех загрязнений.